本文最后更新于 2025年11月14日 晚上
AT_DP_C Vacation
洛谷 Link
有 N N N i i i 1 ≤ i ≤ N 1 \leq i \leq N 1 ≤ i ≤ N
A:在海里游泳,获得幸福度 a i a _ i a i B:在山上抓虫,获得幸福度 b i b _ i b i C:在家做作业,获得幸福度 c i c _ i c i 不能连续两天以上做同样的活动,计算最大总幸福度。
Solution
DP 板子题。设 f i , j f_{i,j} f i , j 截止到第 i i i j j j 。
则易得转移方程为:
f i , 1 = max ( f i − 1 , 2 , f i − 1 , 3 ) f i , 2 = max ( f i − 1 , 1 , f i − 1 , 3 ) f i , 3 = max ( f i − 1 , 1 , f i − 1 , 2 ) f_{i,1}=\max(f_{i-1,2},f_{i-1,3})\\
f_{i,2}=\max(f_{i-1,1},f_{i-1,3})\\
f_{i,3}=\max(f_{i-1,1},f_{i-1,2})
f i , 1 = max ( f i − 1 , 2 , f i − 1 , 3 ) f i , 2 = max ( f i − 1 , 1 , f i − 1 , 3 ) f i , 3 = max ( f i − 1 , 1 , f i − 1 , 2 )
Core Code
1 2 3 4 5 6 for (int i=1 ;i<=n;i++)1 ]=max (f[i-1 ][2 ],f[i-1 ][3 ])+a[i];2 ]=max (f[i-1 ][1 ],f[i-1 ][3 ])+b[i];3 ]=max (f[i-1 ][1 ],f[i-1 ][2 ])+c[i];
AT_DP_K Stones
洛谷 Link
N N N A = { a 1 , a 2 , … , a N } A = \{ a _ 1, a _ 2, \ldots, a _ N \} A = { a 1 , a 2 , … , a N }
首先,准备一个有 K K K
从集合 A A A x x x x x x 不能进行操作的人输掉游戏。当两人都按照最优策略行动时,判断谁会获胜。
Solution
显然当一名玩家操作完成后石子数量为 0 0 0
设 f i f_i f i i i i 1 / 0 1/0 1/0 当前操作的上一步操作必输,当前操作才可以必胜 ,即如果有 a j a_j a j f i − a j = 0 f_{i-a_j}=0 f i − a j = 0 f i = 1 f_i=1 f i = 1
初始化 f 0 = 0 f_0=0 f 0 = 0
f i = { 1 , a j ≤ i , f i − a j = 0 0 , otherwise. f_i=\begin{cases}
1,&a_j\leq i,f_{i-a_j}=0\\
0 ,& \text{otherwise.}
\end{cases}
f i = { 1 , 0 , a j ≤ i , f i − a j = 0 otherwise.
Core Code
1 2 3 4 5 6 7 8 f[0 ]=0 ;for (int i=1 ;i<=k;i++)for (int j=1 ;j<=n;j++)if (i-a[j]>=0 && !f[i-a[j]]) f[i]=1 ;
AT_DP_M Candies
Link
K K K n n n i i i 0 0 0 a i a_i a i 10 9 + 7 10^9+7 1 0 9 + 7
tag: 背包 DP, 前缀和
Solution
类似背包的处理思路,设 f i , j f_{i,j} f i , j i i i j j j ( j − a i ) ∼ j (j-a_i)\sim j ( j − a i ) ∼ j
f i , j = ∑ k = max ( 0 , j − a i ) j f i − 1 , k f_{i,j}=\sum^j_{k=\max(0,j-a_i)}f_{i-1,k}
f i , j = k = m a x ( 0 , j − a i ) ∑ j f i − 1 , k
考虑优化时间,滚动数组不可行。发现每一个 i i i i − 1 i-1 i − 1 i − 1 i-1 i − 1 f f f
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int calc (int l,int r) if (l==0 ) return sum[r];return sum[r]-sum[l-1 ];int main () 0 ][0 ]=1 ;for (int i=1 ;i<=n;i++) {0 ]=f[i-1 ][0 ];for (int j=1 ;j<=m;j++) {-1 ]+f[i-1 ][j]+mod)%mod;for (int j=0 ;j<=m;j++) {calc (max (0ll ,j-a[i]),j)+mod)%mod;printf ("%lld\n" ,f[n][m]%mod);
AT_DP_P Independent Set
Link
给一棵树,每一个点可以染成黑色或白色,任意两个相邻节点不能都是黑色,求方案数。
tag: 树形 DP
Solution
设 f u , 0 / 1 f_{u,0/1} f u , 0/1 u u u
f u , 0 = ∏ v ∈ u ( f v , 0 + f v , 1 ) f u , 1 = ∏ v ∈ u f v , 0 \begin{aligned}
f_{u,0}&=\prod_{v\in u}(f_{v,0}+f_{v,1})\\
f_{u,1}&=\prod_{v\in u}f_{v,0}
\end{aligned}
f u , 0 f u , 1 = v ∈ u ∏ ( f v , 0 + f v , 1 ) = v ∈ u ∏ f v , 0
注意 1 1 1
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 void dfs (int u) 1 ;0 ]=f[u][1 ]=1 ;for (int i=0 ;i<e[u].size ();i++) {int v=e[u][i];if (!g.vis[v]) {dfs (v);0 ]=(f[u][0 ]*(f[v][0 ]+f[v][1 ]))%mod;1 ]=(f[u][1 ]*f[v][0 ])%mod;
AT_DP_Q Flowers
Link
有一排花,共 n n n i i i h i h_i h i a i a_i a i
tag: 线段树优化 DP
Solution
带权的最长上升子序列,设 f i f_i f i i i i
f i = max j = 1 i − 1 { f j ∣ h j < h i } + a i f_{i}=\max_{j=1}^{i-1}\{f_{j}|h_j<h_i\}+a_{i}
f i = j = 1 max i − 1 { f j ∣ h j < h i } + a i
考虑优化,观察到转移方程是区间最大值,想到用值域线段树优化。将 h i h_i h i f i f_i f i
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 struct node {4 ];struct tree {void pushup (int p) max (t[p * 2 ].val, t[p * 2 + 1 ].val);void modify (int p, int l, int r, int x, ll k) if (l == r) {return ;int mid = (l + r) >> 1 ;if (x <= mid) modify (p * 2 , l, mid, x, k);else modify (p * 2 + 1 , mid + 1 , r, x, k);pushup (p);ll query (int p, int l, int r, int x, int y) {if (x <= l && r <= y) {return t[p].val;0 ;int mid = (l + r) >> 1 ;if (x <= mid) res = max (res, query (p * 2 , l, mid, x, y));if (y >= mid + 1 ) res = max (res, query (p * 2 + 1 , mid + 1 , r, x, y));return res;int main () read ();for (int i = 1 ; i <= n; i++) {read ();for (int i = 1 ; i <= n; i++) {read ();for (int i = 1 ; i <= n; i++) {query (1 , 1 , n, 1 , h[i]) + a[i];modify (1 , 1 , n, h[i], f[i]);query (1 , 1 , n, 1 , n) << endl;return 0 ;
AT_DP_T Permutation
Link
有一个长为 N N N < 和 > 组成长为 N − 1 N-1 N − 1 1 ≤ i ≤ N − 1 1 \le i \le N-1 1 ≤ i ≤ N − 1 s i s_i s i s i s_i s i < 则 P i < P i + 1 P_i<P_{i+1} P i < P i + 1 s i s_i s i > 则 P i > P i + 1 P_i>P_{i+1} P i > P i + 1 P P P
Solution
由于 p p p p p p f i , j f_{i, j} f i , j i i i i i i j j j
在转移时,若当前填的数需大于前一个数,那么直接得到 f i , j = ∑ k = 1 j − 1 f i − 1 , k \displaystyle f_{i,j}=\sum_{k=1}^{j-1}f_{i-1,k} f i , j = k = 1 ∑ j − 1 f i − 1 , k
若小于前一个数,有 f i , j = ∑ k = j i − 1 f i − 1 , k \displaystyle f_{i,j}=\sum_{k=j}^{i-1}f_{i-1,k} f i , j = k = j ∑ i − 1 f i − 1 , k j j j 1 ∼ i − 1 1\sim i-1 1 ∼ i − 1 j − 1 j-1 j − 1 j j j j j j j ∼ i − 1 j\sim i-1 j ∼ i − 1
注意到转移是求连续一段的和,前缀和优化即可。
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 sum[1 ] = 1 ;for (int i = 2 ; i <= n; i++) {for (int j = 1 ; j <= n; j++) {if (s[i - 1 ] == '<' ) {1 ] - sum[j - 1 ] + mod) % mod;else {1 ] % mod;for (int j = 1 ; j <= n; j++) {1 ] + f[j]) % mod;int ans = 0 ;for (int i = 1 ; i <= n; i++) {'\n' ;
AT_DP_W Intervals
Link
给定 m m m ( l i , r i , a i ) (l_i,r_i,a_i) ( l i , r i , a i ) i i i [ l i , r i ] [l_i,r_i] [ l i , r i ] a i a_i a i
你需要求出长度为 n n n
tag: 线段树优化 DP, 区间右端点排序
Solution
首先将区间按右端点排序,在右端点处统计答案。
考虑 DP,设 f i , j f_{i,j} f i , j i i i 1 1 1 j j j
不难想到 f i , j = max k = 1 j f i − 1 , k + ∑ l p ≤ k and r p = i a p \displaystyle f_{i,j}=\max_{k=1}^j f_{i-1,k}+\sum_{l_p\leq k\text{ and }r_p=i} a_p f i , j = k = 1 max j f i − 1 , k + l p ≤ k and r p = i ∑ a p [ l , r ] [l, r] [ l , r ] k k k
对上式进行优化,发现可以贪心的使 1 1 1 1 1 1 f i , j = f i − 1 , j + ∑ l k ≤ j and r k = i a k \displaystyle f_{i,j}=f_{i-1,j}+\sum_{l_k\leq j\text{ and }r_k=i}a_k f i , j = f i − 1 , j + l k ≤ j and r k = i ∑ a k
优化后,会有 j = i j=i j = i 1 1 1
f i , j = { max k = 1 j − 1 f i − 1 , k + ∑ r p = i a p , i = j f i − 1 , j + ∑ l k ≤ j and r k = i a k , i ≠ j f_{i,j}=
\begin{cases}
\max_{k=1}^{j-1} f_{i-1,k}+\sum_{r_p=i} a_p,&i=j\\
f_{i-1,j}+\sum_{l_k\leq j\text{ and }r_k=i} a_k,&i\neq j
\end{cases}
f i , j = { max k = 1 j − 1 f i − 1 , k + ∑ r p = i a p , f i − 1 , j + ∑ l k ≤ j and r k = i a k , i = j i = j
滚动掉一维后,发现枚举位置 i i i r j = i r_j=i r j = i [ l j , r j ] [l_j, r_j] [ l j , r j ] [ l j , i ] [l_j, i] [ l j , i ] a j a_j a j
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 struct query {int l, r, a;bool operator <(const query &x) const {return r < x.r;struct node {int val, tag;struct tree {4 * N];void mktag (int p, int w) void pushdown (int p) if (t[p].tag) {mktag (p * 2 , t[p].tag);mktag (p * 2 + 1 , t[p].tag);0 ;void pushup (int p) max (t[p * 2 ].val, t[p * 2 + 1 ].val);void modify (int p, int l, int r, int x, int y, int w) if (x <= l && r <= y) {mktag (p, w);return ;pushdown (p);int mid = (l + r) >> 1 ;if (x <= mid) modify (p * 2 , l, mid, x, y, w);if (y >= mid + 1 ) modify (p * 2 + 1 , mid + 1 , r, x, y, w);pushup (p);int query (int p, int l, int r, int x, int y) if (x <= l && r <= y) {return t[p].val;pushdown (p);int mid = (l + r) >> 1 ;int res = 0 ;if (x <= mid) res = max (res, query (p * 2 , l, mid, x, y));if (y >= mid + 1 ) res = max (res, query (p * 2 + 1 , mid + 1 , r, x, y));return res;signed main () read (); m = read ();for (int i = 1 ; i <= m; i++) {read (), q[i].r = read (), q[i].a = read ();sort (q + 1 , q + m + 1 );int nw = 1 ;for (int i = 1 ; i <= n; i++) {if (i != 1 ) sgt.modify (1 , 1 , n, i, i, sgt.query (1 , 1 , n, 1 , i - 1 ));while (q[nw].r == i && nw <= m) {modify (1 , 1 , n, q[nw].l, i, q[nw].a);max (0ll , sgt.query (1 , 1 , n, 1 , n)) << endl;return 0 ;
TDPC_IWI イウィ
洛谷 Link
给定一个仅由字符 i \texttt{i} i w \texttt{w} w s s s iwi \texttt{iwi} iwi 3 3 3
tag: 区间 DP
Solution
区间 DP,类似合并石子。
我们定义 f i , j f_{i,j} f i , j i i i j j j 3 3 3
因为答案计算的是最大的步数,那么对于一个大区间,在一般情况下的答案就应该是其分成的两个小区间的答案之和。考虑枚举这两个区间之间的分界点 k k k
本题还需要特判一种特殊情况。如果 s i s_i s i s j s_j s j i,s k s_k s k w,且中间的两个小段可以被完全删除。那么,当中间的被删掉之后,左右的 i 和中间的 w 就会拼在一起,也可以删掉,那么这个区间的答案就应该是它的长度,但显然直接相加有可能会出错。
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 for (int a=2 ;a<=len;a++)for (int i=1 ;a+i-1 <=len;i++)int j=a+i-1 ;for (int k=i;k<j;k++)max (f[i][j],f[i][k]+f[k+1 ][j]);if (s[i]=='i' && s[j]=='i' && s[k]=='w' && f[i+1 ][k-1 ] == k-i-1 && f[k+1 ][j-1 ] == j-1 -k)+1 ;write (f[1 ][len]/3 );
ABC247F Cards
Link
给定 n n n 1 1 1 n n n 1 1 1 n n n 998244353 998244353 998244353
tag: 并查集
Solution
trick 题,记住。
想到在两个拥有相同数字的卡片连边,则一个边的两点中必须至少选一个。
由于每张卡有两个数,度数为二,则连完后必定会形成若干个简单环或自环。
根据乘法原理,对于每个环求出方案数后相乘后即为答案。
先上结论,设 f i f_i f i i i i
f i = f i − 1 + f i − 2 f_i=f_{i-1}+f_{i-2}
f i = f i − 1 + f i − 2
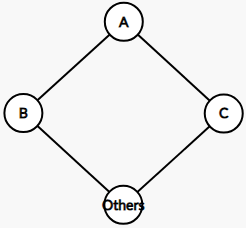
考虑证明它,设一个如下图的环,其中 others 表示剩余的所有点。
分类讨论,如果选 A A A B B B C C C A A A B B B C C C f i − 1 f_{i-1} f i − 1 B B B C C C B B B C C C k k k
如果不选 A A A B B B C C C B B B C C C f i − 2 f_{i-2} f i − 2 B B B C C C k k k
所以可以得到:
f i = f i − 1 + k̸ + f i − 2 − k̸ f_i=f_{i-1}+\not k+f_{i-2}-\not k
f i = f i − 1 + k + f i − 2 − k
用并查集存环即可。
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 n = read ();for (int i = 1 ; i <= n; i++) fa[i] = i;for (int i = 1 ; i <= n; i++) {read ()] = i;for (int i = 1 ; i <= n; i++) {read ();merge (i, t[ q[i] ]);for (int i = 1 ; i <= n; i++) {find (i)]++;1 ] = 1ll , f[2 ] = 3ll ;for (int i = 3 ; i < N; i++) {1 ] + f[i - 2 ]) % mod;int ans = 1ll ;0 ] = 1ll ;for (int i = 1 ; i <= n; i++) {
ABC336D Pyramid
Link
对于正整数 k k k k k k 2 k − 1 2k-1 2 k − 1 1 , 2 , 3 , … k − 1 , k , k − 1 , … 3 , 2 , 1 1,2,3,\dots k-1,k,k-1,\dots 3,2,1 1 , 2 , 3 , … k − 1 , k , k − 1 , … 3 , 2 , 1 n n n S S S
选择一个数 i ( 1 ≤ i ≤ n ) i(1 \le i \le n) i ( 1 ≤ i ≤ n ) S i S_i S i 1 1 1 删除整个数列的第一个或最后一个数字。 问最后生成的“金字塔数列”的最大的 k k k
Solution
显然一个金字塔数列是由左右两部分拼接而成的。设 f i f_{i} f i i i i g i g_{i} g i i i i i i i x x x x − 1 x-1 x − 1 i i i min { f i , g i } \min\{f_i, g_i\} min { f i , g i }
以 f f f s i s_i s i + ∞ +\infty + ∞ f i = f i − 1 + 1 f_{i}=f_{i-1}+1 f i = f i − 1 + 1 s i s_i s i f i = min { f i − 1 + 1 , s i } f_i=\min\{f_{i-1}+1, s_i\} f i = min { f i − 1 + 1 , s i } g i = min { g i + 1 + 1 , s i } g_i=\min\{g_{i+1}+1, s_i\} g i = min { g i + 1 + 1 , s i }
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 n = read ();for (int i = 1 ; i <= n; i++) {read ();1 ] = g[n] = 1 ;for (int i = 2 ; i <= n; i++) {min (f[i-1 ] + 1 , a[i]);for (int i = n - 1 ; i >= 1 ; i--) {min (g[i+1 ] + 1 , a[i]);int ans = 0 ;for (int i = 1 ; i <= n; i++) {max (ans, min (f[i], g[i]));
SP703 Mobile Service
Problem Link
有 3 3 3 2 2 2
从位置 p p p q q q c ( p , q ) c(p,q) c ( p , q ) c ( i , i ) = 0 c(i,i)=0 c ( i , i ) = 0 c ( p , q ) = c ( q , p ) c(p,q)=c(q,p) c ( p , q ) = c ( q , p )
现在给出 N N N i i i x i x_i x i x i x_i x i
3 3 3 1 , 2 , 3 1,2,3 1 , 2 , 3
求公司的最小花费。
tag: DP
Solution
设 f i , x , y , z f_{i,x,y,z} f i , x , y , z i i i x , y , z x,y,z x , y , z f i , x , y f_{i,x,y} f i , x , y z = q i − 1 z=q_{i-1} z = q i − 1
f i + 1 , x , y = min ( f i + 1 , x , y , f i , x , y + c z , q i + 1 ) f i + 1 , x , z = min ( f i + 1 , x , z , f i , x , y + c y , q i + 1 ) f i + 1 , y , z = min ( f i + 1 , y , z , f i , x , y + c x , q i + 1 ) f_{i+1,x,y}=\min(f_{i+1,x,y},f_{i,x,y}+c_{z,q_{i+1}})\\
f_{i+1,x,z}=\min(f_{i+1,x,z},f_{i,x,y}+c_{y,q_{i+1}})\\
f_{i+1,y,z}=\min(f_{i+1,y,z},f_{i,x,y}+c_{x,q_{i+1}})
f i + 1 , x , y = min ( f i + 1 , x , y , f i , x , y + c z , q i + 1 ) f i + 1 , x , z = min ( f i + 1 , x , z , f i , x , y + c y , q i + 1 ) f i + 1 , y , z = min ( f i + 1 , y , z , f i , x , y + c x , q i + 1 )
初值 q 0 = 1 , f 0 , 2 , 3 = 0 q_0=1, f_{0,2,3}=0 q 0 = 1 , f 0 , 2 , 3 = 0
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 for (int i=0 ;i<n;i++) {for (int x=1 ;x<=l;x++) {for (int y=1 ;y<=l;y++) {int z=q[i];if (x==y || x==z || y==z) continue ;+1 ][x][y]=min (f[i+1 ][x][y],f[i][x][y]+c[z][q[i+1 ]]);+1 ][z][y]=min (f[i+1 ][z][y],f[i][x][y]+c[x][q[i+1 ]]);+1 ][x][z]=min (f[i+1 ][x][z],f[i][x][y]+c[y][q[i+1 ]]);int ans=INF;for (int x=1 ;x<=l;x++) {for (int y=1 ;y<=l;y++) {int z=q[n];if (x==y || x==z || y==z) continue ;min (ans,f[n][x][y]);
P4310 绝世好题
Link 和同类题 CF264B Good Sequences
给定一个长度为 n n n a i a_i a i a i a_i a i b i b_i b i k k k b i and b i − 1 ≠ 0 b_i\ \text{and}\ b_{i-1} \neq 0 b i and b i − 1 = 0 2 ≤ i ≤ k 2\leq i\leq k 2 ≤ i ≤ k
tag: 位运算, DP
Solution
设 f i f_{i} f i a i a_i a i bit i \text{bit}_i bit i i i i 1 1 1
可以注意到只要两个数同一二进制位都为 1 1 1 0 0 0 ( 1000 ) 2 and ( 1010 ) 2 and ( 0010 ) 2 ≠ 0 (1000)_2\ \text{and}\ (1010)_2\ \text{and}\ (0010)_2\neq 0 ( 1000 ) 2 and ( 1010 ) 2 and ( 0010 ) 2 = 0
所以在每次循环时,先通过枚举 a i a_i a i f i f_i f i f i f_i f i a i a_i a i 1 1 1 bit i \text{bit}_i bit i
{ f i = max ( f i , bit j ) bit j = f i , a i and ( 1 < < j ) ≠ 0 \begin{cases}
f_i&=\max(f_i, \text{bit}_j)\\
\text{bit}_j&=f_i
\end{cases}
, a_i\ \text{and}\ (1<<j)\neq 0
{ f i bit j = max ( f i , bit j ) = f i , a i and ( 1 << j ) = 0
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 for (int i=1 ;i<=n;i++) {for (int j=0 ;j<=32 ;j++) {if ((1 <<j)&a[i]) f[i]=max (f[i],bit[j]+1 );for (int j=0 ;j<=32 ;j++) {if ((1 <<j)&a[i]) bit[j]=f[i];int ans=0 ;for (int i=1 ;i<=n;i++) {max (ans,f[i]);
P1944 最长括号匹配
Problem Link
对一个由 (,),[,] 括号组成的字符串,求出其中最长的括号匹配子串。
(),[] 是括号匹配的字符串。 若 A 是括号匹配的串,则 (A),[A] 是括号匹配的字符串。 若 A,B 是括号匹配的字符串,则 AB 也是括号匹配的字符串。 例如:(),[],([]),()() 都是括号匹配的字符串,而 ][,[(]) 则不是。
字符串 A 的子串是指由 A 中连续若干个字符组成的字符串,包含空串。
Solution
设 f i f_i f i s i s_i s i
显然,当且仅当在其 前面括号匹配长度(f i − 1 f_{i-1} f i − 1 (xxx))。
由此可得式子 f i = f i − 1 + f i − f i − 1 − 2 + 2 f_i=f_{i-1}+f_{i-f_{i-1}-2}+2 f i = f i − 1 + f i − f i − 1 − 2 + 2 i − f i − 1 − 2 i-f_{i-1}-2 i − f i − 1 − 2
Core Code
1 2 3 4 5 6 7 8 9 10 11 for (int i=1 ;i<=n;i++) {if ((s[i]==')' && s[i-f[i-1 ]-1 ]=='(' ) || (s[i]==']' && s[i-f[i-1 ]-1 ]=='[' )) f[i]=f[i-1 ]+f[i-f[i-1 ]-2 ]+2 ;if (ans<f[i]) {for (int i=last-ans+1 ;i<=last;i++) {putchar (s[i]);
P1284 三角形牧场
Problem Link
给定多个线段,求全部使用情况下最大能围成的三角形周长。
tag: 背包
Solution
显然要用海伦公式求周长,那就需要枚举三角形三条边的长度。由于所有边都需要使用,可以优化为仅枚举两条边的长度。
设 f k , i , j f_{k,i,j} f k , i , j k k k i , j i, j i , j
类似 01 背包思路,f k f_k f k f k − 1 f_{k-1} f k − 1 i , j i,j i , j f k − 1 , i − l k , j , f k − 1 , i , j − l k , f k − 1 , i , j f_{k-1, i-l_k, j}, f_{k-1, i, j-l_k}, f_{k-1, i, j} f k − 1 , i − l k , j , f k − 1 , i , j − l k , f k − 1 , i , j
f k , i , j = { true , f k − 1 , i − l k , j = true or f k − 1 , i , j − l k = true or f k − 1 , i , j = true false , otherwise. f_{k,i,j}=
\begin{cases}
\text{true}, &f_{k-1,i-l_k,j}=\text{true}\ \text{or}\ f_{k-1,i,j-l_k}=\text{true}\
\text{or}\ f_{k-1,i,j}=\text{true}\\
\text{false}, &\text{otherwise.}
\end{cases}
f k , i , j = { true , false , f k − 1 , i − l k , j = true or f k − 1 , i , j − l k = true or f k − 1 , i , j = true otherwise.
同 01 背包一样,k k k
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 bool check (int a,int b,int c) if (a+b>c && a+c>b && b+c>a) return 1 ;else return 0 ;double calc (double a,double b,double c) double p=(a+b+c)/2.0 ;return 100.0 *sqrt (p*(p-a)*(p-b)*(p-c));int main () 0 ][0 ]=1 ;for (int i=1 ;i<=n;i++) {for (int j=p;j>=0 ;j--) {for (int k=p;k>=0 ;k--) {if (j-l[i]>=0 && f[j-l[i]][k]) f[j][k]=1 ;if (k-l[i]>=0 && f[j][k-l[i]]) f[j][k]=1 ;int ans=-1 ;for (int i=1 ;i<=p;i++) {for (int j=1 ;j<=p;j++) {if (check (i,j,p-i-j) && f[i][j]) ans=max (ans,(int )calc (i,j,p-i-j));
P4084 [USACO17DEC] Barn Painting G
Problem Link
给定一颗 N N N K K K
tag: 树形 dp
Solution
树形 DP,设 f i , j f_{i,j} f i , j i i i j j j
若 i i i j j j f i , j = 1 f_{i,j}=1 f i , j = 1 0 0 0 f i , j = 1 , j ∈ [ 1 , 3 ] f_{i,j}=1, j\in [1,3] f i , j = 1 , j ∈ [ 1 , 3 ]
从下向上转移:
{ f u , 1 = ∏ v ∈ son ( u ) ( f v , 2 + f v , 3 ) f u , 2 = ∏ v ∈ son ( u ) ( f v , 1 + f v , 3 ) f u , 3 = ∏ v ∈ son ( u ) ( f v , 1 + f v , 2 ) \begin{cases}
f_{u,1}=\prod_{v\in \text{son}(u)} (f_{v,2}+f_{v,3})\\
f_{u,2}=\prod_{v\in \text{son}(u)} (f_{v,1}+f_{v,3})\\
f_{u,3}=\prod_{v\in \text{son}(u)} (f_{v,1}+f_{v,2})
\end{cases}
⎩ ⎨ ⎧ f u , 1 = ∏ v ∈ son ( u ) ( f v , 2 + f v , 3 ) f u , 2 = ∏ v ∈ son ( u ) ( f v , 1 + f v , 3 ) f u , 3 = ∏ v ∈ son ( u ) ( f v , 1 + f v , 2 )
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #define int ll int > e[N];int n,k;int f[N][5 ];bool is_colored[N];bool vis[N];void dfs (int u) 1 ;for (int i=0 ;i<e[u].size ();i++) {int v=e[u][i];if (!vis[v]) {dfs (v);1 ]=(f[u][1 ]*((f[v][2 ]+f[v][3 ]+mod)%mod)+mod)%mod;2 ]=(f[u][2 ]*((f[v][1 ]+f[v][3 ]+mod)%mod)+mod)%mod;3 ]=(f[u][3 ]*((f[v][1 ]+f[v][2 ]+mod)%mod)+mod)%mod;signed main () read ();k=read ();for (int i=1 ;i<n;i++) {int u=read (),v=read ();push_back (v);push_back (u);for (int i=1 ;i<=k;i++) {int b=read (),c=read ();1 ;1 ;for (int i=1 ;i<=n;i++) {if (!is_colored[i]) f[i][1 ]=f[i][2 ]=f[i][3 ]=1 ;dfs (1 );printf ("%lld\n" ,(f[1 ][1 ]+f[1 ][2 ]+f[1 ][3 ]+mod)%mod);return 0 ;
P2458 [SDOI2006] 保安站岗
Link
给定一颗树,每个点有点权 k k k
tag: 树形 DP
与 P2016 战略游戏 不同,本题为守点。如 1-2-3-4 本题可以选择 1 和 4,但战略游戏不可。所以本题需要设这三个状态。
本题守点,意味着如果一个点不选,那么只需要与这个点相连的任一点选择即可,而守边则就需要与这个点相连的所有点都选。
Solution
首先不能将状态设为一个点被占或不占,这样会造成向上转移时父节点无法影响子节点。
设 f u , 1 / 2 / 3 f_{u,1/2/3} f u , 1/2/3 u u u
首先第一种情况显然 f u , 1 = ∑ v ∈ son ( u ) min ( f v , 1 , f v , 2 , f v , 3 ) + k u f_{u,1}=\sum_{v\in \text{son}(u)}\min(f_{v,1}, f_{v,2}, f_{v,3})+k_u f u , 1 = ∑ v ∈ son ( u ) min ( f v , 1 , f v , 2 , f v , 3 ) + k u
对于第三种情况,由于 u u u u u u v v v v v v v v v f u , 3 = ∑ v ∈ son ( u ) min ( f v , 1 , f v , 2 ) f_{u,3}=\sum_{v\in \text{son}(u)}\min(f_{v,1}, f_{v,2}) f u , 3 = ∑ v ∈ son ( u ) min ( f v , 1 , f v , 2 )
对于第二种情况,分析方式类似第三种,首先要满足子树被覆盖。同时,要有至少一个 v v v u u u f v , 2 f_{v,2} f v , 2 v v v f v , 1 f_{v,1} f v , 1
最终答案即为 min ( f root , 1 , f root , 2 ) \min(f_{\text{root},1}, f_{\text{root},2}) min ( f root , 1 , f root , 2 )
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 void dfs (int u,int fa) int minn=INF;bool flag=0 ;for (auto v:e[u]) {if (v==fa) continue ;dfs (v,u);1 ]+=min (f[v][1 ],min (f[v][2 ],f[v][3 ]));2 ]+=min (f[v][1 ],f[v][2 ]);3 ]+=min (f[v][1 ],f[v][2 ]);min (minn,f[v][1 ]-f[v][2 ]);if (f[v][1 ]<f[v][2 ]) flag=1 ;if (!flag) f[u][2 ]+=minn;int main () read ();for (int i=1 ;i<=n;i++) {int u=read ();read ();int m=read ();1 ]=k[u];for (int j=1 ;j<=m;j++) {int v=read ();push_back (v);push_back (u);dfs (1 ,0 );min (f[1 ][1 ],f[1 ][2 ])<<endl;return 0 ;
P2016 战略游戏
Link
给定一颗树,一个节点可以看守相邻的所有边,求看守整棵树需要的最少的节点数。
tag: 树形 DP
本题与上一题不用的是,本题可以转化为一个点可以看守与这个点相连的所有边。
本题守边,意味着如果一个点不选,那么就需要与这个点相连的所有点都选,而守点则只需要与这个点相连的任一点选择即可。
Solution
设 f u , 0 / 1 f_{u,0/1} f u , 0/1 u u u
如果 u u u f u , 0 = ∑ v ∈ son ( u ) f v , 1 f_{u,0}=\sum_{v\in \text{son}(u)} f_{v,1} f u , 0 = ∑ v ∈ son ( u ) f v , 1
如果 u u u f u , 0 = ∑ v ∈ son ( u ) min { f v , 0 , f v , 1 } f_{u,0}=\sum_{v\in \text{son}(u)}\min\{f_{v,0}, f_{v,1}\} f u , 0 = ∑ v ∈ son ( u ) min { f v , 0 , f v , 1 }
Core Code
1 2 3 4 5 6 7 8 9 void dfs (int u,int fa) 1 ]=1 ;for (auto v:e[u]) {if (v==fa) continue ;dfs (v,u);0 ]+=f[v][1 ];1 ]+=min (f[v][0 ],f[v][1 ]);
P3478 [POI2008] STA-Station
Link
给出一个 n n n
tag: 树形 DP, 换根 DP
Solution
换根板子。
首先考虑如何暴力,显然是以每个点为根都跑一边 dfs,时间复杂度 O ( n 2 ) \mathcal O(n^2) O ( n 2 )
一般换根 DP 题的处理思路是:
先指定一个根节点,一次 dfs 自下而上,用子节点的值更新父节点;
从上一步的根出发,dfs 转移父节点对子节点的贡献。
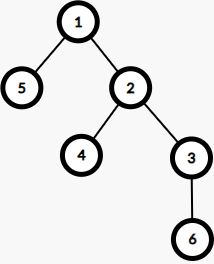
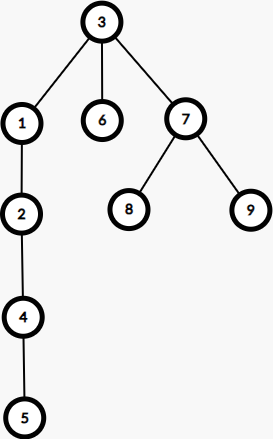
设 f u f_{u} f u u u u u u u 2 2 2 4 4 4 4 4 4 1 1 1 4 4 4 1 1 1
可以得到转移方程:
f v = f u − siz v × 1 + ( n − siz v ) × 1 = f u + n − 2 × siz v f_{v}=f_{u}-\text{siz}_{v}\times 1+(n-\text{siz}_{v})\times 1=f_u+n-2\times \text{siz}_v
f v = f u − siz v × 1 + ( n − siz v ) × 1 = f u + n − 2 × siz v
其中 siz v × 1 \text{siz}_v\times 1 siz v × 1 4 4 4 n − siz v n-\text{siz}_v n − siz v 4 4 4
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 void dfs1 (int u,int fa) 1 ;for (auto v:e[u]) {if (v==fa) continue ;+1 ;dfs1 (v,u);void dfs2 (int u,int fa) for (auto v:e[u]) {if (v==fa) continue ;-2ll *g.siz[v];dfs2 (v,u);int main () dfs1 (1 ,0 );for (int i=2 ;i<=n;i++) {1 ]+=g.dep[i];dfs2 (1 ,0 );for (int i=1 ;i<=n;i++) {if (maxn<f[i]) {return 0 ;
P3047 [USACO12FEB] Nearby Cows G
Link
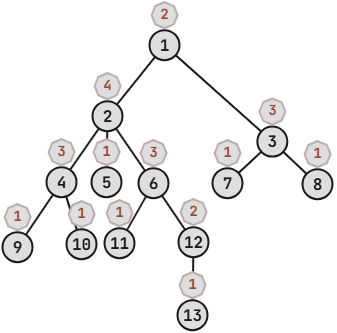
给你一棵 n n n k k k m i m_i m i
tag: 换根 DP
Solution
设 f u , d f_{u,d} f u , d u u u k k k
两边 dfs,第一遍向上转移,计算子树对当前节点的贡献。注意到与 u u u k k k k − 1 k-1 k − 1 f u , d = ∑ v ∈ son ( u ) f v , d − 1 f_{u,d}=\sum_{v\in \text{son}(u)} f_{v,d-1} f u , d = ∑ v ∈ son ( u ) f v , d − 1
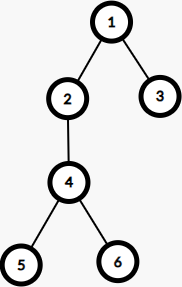
第二遍时计算父亲对当前节点的贡献。同样可以由一的思路 f v , d = f u , d − 1 ( v ∈ son ( u ) ) f_{v,d}=f_{u,d-1}(v\in \text{son}(u)) f v , d = f u , d − 1 ( v ∈ son ( u )) u u u d d d v v v d − 1 d-1 d − 1 f 2 , 2 f_{2,2} f 2 , 2 f 3 , 1 f_{3,1} f 3 , 1 f v , d − 2 f_{v,d-2} f v , d − 2
注意在进行第二遍 dfs 时,要注意循环顺序,防止容斥后的 f f f
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void dfs1 (int u, int fa) for (auto v : e[u]) {if (v == fa) continue ;dfs1 (v, u);for (int d = 1 ; d <= k; d++) {-1 ];void dfs2 (int u, int fa) for (auto v : e[u]) {if (v == fa) continue ;for (int d = 1 ; d <= k; d++) {-1 ];for (int d = k; d >= 2 ; d--) {-2 ];dfs2 (v, u);
CF474E Pillars
Link
给定序列长度为 n n n a a a d d d
找出一个最长的 a a a b b b m m m 1 ≤ i < m 1\le i\lt m 1 ≤ i < m ∣ b i + 1 − b i ∣ ≥ d |b_{i+1}-b_i|\ge d ∣ b i + 1 − b i ∣ ≥ d
输出 m m m b b b a a a
tag: 动态开点线段树, 线段树优化 DP
Solution
设 f i f_i f i i i i
f i = max ∣ b i − b j ∣ ≥ d { f j } + 1 = max 1 ≤ j ≤ a i − d or a i + d ≤ j ≤ n { f j } + 1 \begin{aligned}
f_i &= \max_{\lvert b_i - b_j\rvert \geq d}\{f_j\} + 1\\
&=\max_{1\leq j\leq a_i - d\ \text{or}\ a_i + d\leq j\leq n}\{f_j\} + 1
\end{aligned}
f i = ∣ b i − b j ∣ ≥ d max { f j } + 1 = 1 ≤ j ≤ a i − d or a i + d ≤ j ≤ n max { f j } + 1
考虑线段树优化掉两部分区间最值。使用权值线段树,每次计算完 i i i f i f_i f i a i a_i a i
数据范围过大,需动态开点或离散化。
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 int n, d;int tot = 0 ;int rt;struct pr {int val, id;bool operator < (pr const & x) {return val < x.val;pr max (pr x, pr y) {if (x < y) return y;else return x;struct node {int l, r;40 * N];struct tree {void pushup (int p) max (t[t[p].l].val, t[t[p].r].val);void modify (int &p, int l, int r, int x, pr w) if (!p) p = ++tot;if (l == r) {if (t[p].val < w) t[p].val = w;return ;int mid = (l + r) >> 1 ;if (x <= mid) modify (t[p].l, l, mid, x, w);else modify (t[p].r, mid + 1 , r, x, w);pushup (p);pr query (int p, int l, int r, int x, int y) {if (!p || y < x) return {0 , 0 };if (x <= l && r <= y) {return t[p].val;int mid = (l + r) >> 1 ;0 };if (x <= mid) res = max (res, query (t[p].l, l, mid, x, y));if (y >= mid + 1 ) res = max (res, query (t[p].r, mid + 1 , r, x, y));return res;signed main () read (); d = read ();for (int i = 1 ; i <= n; i++) {read ();0 , 0 };for (int i = 1 ; i <= n; i++) {max (sgt.query (rt, 1 , MAXN, 1 , a[i].val - d),query (rt, 1 , MAXN, a[i].val + d, MAXN));bug (f[i].id);1 ;max (maxn, {f[i].val, i});modify (rt, 1 , MAXN, a[i].val, {f[i].val, i});int > st;for (int i = maxn.id; i >= 1 ; i = f[i].id) {bug (f[i].id);push (i);while (!st.empty ()) {top () << " " ;pop ();return 0 ;
CF708C Centroids
Link
给定一颗树,你有一次将树改造的机会,改造的意思是删去一条边,再加入一条边,保证改造后还是一棵树。
请问有多少点可以通过改造,成为这颗树的重心?(如果以某个点为根,每个子树的大小都不大于 n 2 \dfrac{n}{2} 2 n
tag: 树形 DP, 换根 DP
Solution
根据重心的定义,如果一个点 u u u s i z > ⌊ n 2 ⌋ siz > \lfloor\frac{n}{2}\rfloor s i z > ⌊ 2 n ⌋ u u u u u u
如果先将一个不需要操作即可满足条件的节点钦定为根,那么这棵树的所有子树都满足 s i z ≤ ⌊ n 2 ⌋ siz\leq \lfloor\frac{n}{2}\rfloor s i z ≤ ⌊ 2 n ⌋
所以,若在这棵新树上进行 DP,对于任何一个节点 u u u n − s i z u n - siz_u n − s i z u g u g_u g u u u u ⌊ n 2 ⌋ \lfloor\frac{n}{2}\rfloor ⌊ 2 n ⌋ u u u
那么,只需要判断除了上面这两部分一定合法的,剩下的那些点是否合法,即 n − s i z u − g u ≤ ⌊ n 2 ⌋ n - siz_u - g_u \leq \lfloor\frac{n}{2}\rfloor n − s i z u − g u ≤ ⌊ 2 n ⌋
也就是说,问题转化为求 g u g_u g u
考虑自上而下转移,g u g_u g u f a u fa_u f a u g f a u g_{fa_u} g f a u f u f_u f u u u u ⌊ n 2 ⌋ \lfloor\frac{n}{2}\rfloor ⌊ 2 n ⌋ g u g_u g u f f a u f_{fa_u} f f a u u u u f u , 0 f_{u, 0} f u , 0 f u , 1 f_{u, 1} f u , 1
显然 f u , 0 f_{u, 0} f u , 0
f u , 0 = { f v , 0 , siz v > ⌊ n 2 ⌋ siz u , siz v ≤ ⌊ n 2 ⌋ f_{u, 0}=
\begin{cases}
f_{v, 0}, &\text{siz}_v >\lfloor\frac{n}{2}\rfloor\\
\text{siz}_u, &\text{siz}_v \leq\lfloor\frac{n}{2}\rfloor
\end{cases}
f u , 0 = { f v , 0 , siz u , siz v > ⌊ 2 n ⌋ siz v ≤ ⌊ 2 n ⌋
可以按下面的 trick 维护次大值,为了表示方便,用 x x x
{ f u , 1 = f u , 0 , f u , 0 = x , f u , 0 < x f u , 1 = x , f u , 0 ≤ x < f u , 1 \begin{cases}
f_{u, 1} = f_{u, 0}, f_{u, 0} = x, &f_{u, 0} < x\\
f_{u, 1} = x, &f_{u, 0}\leq x < f_{u, 1}
\end{cases}
{ f u , 1 = f u , 0 , f u , 0 = x , f u , 1 = x , f u , 0 < x f u , 0 ≤ x < f u , 1
然后即可自上而下转移 g u g_u g u
g v = max { f u , 1 , f u , 0 = siz v f u , 0 , f u , 0 ≠ siz v g u n − siz v , n − siz v ≤ ⌊ n 2 ⌋ g_v=\max
\begin{cases}
f_{u, 1}, &f_{u, 0} = \text{siz}_v\\
f_{u, 0}, &f_{u, 0} \neq \text{siz}_v\\
g_u\\
n - \text{siz}_v, &n - \text{siz}_v \leq \lfloor\frac{n}{2}\rfloor
\end{cases}
g v = max ⎩ ⎨ ⎧ f u , 1 , f u , 0 , g u n − siz v , f u , 0 = siz v f u , 0 = siz v n − siz v ≤ ⌊ 2 n ⌋
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 void findrt (int u, int fa) for (auto v : e[u]) {if (v == fa) continue ;findrt (v, u);if (siz[v] > n / 2 ) return ;if (n - siz[u] > n / 2 ) return ;void dfs1 (int u, int fa) for (auto v : e[u]) {if (v == fa) continue ;dfs1 (v, u);if (siz[v] > n / 2 ) {if (f[v][0 ] > f[u][0 ]) {1 ] = f[u][0 ];0 ] = f[v][0 ];else if (f[v][0 ] > f[u][1 ]) {1 ] = f[v][0 ];else {if (siz[v] > f[u][0 ]) {1 ] = f[u][0 ];0 ] = siz[v];else if (siz[v] > f[u][1 ]) {1 ] = siz[v];void dfs2 (int u, int fa) for (auto v : e[u]) {if (v == fa) continue ;max (g[v], g[u]);if (n - siz[v] <= n / 2 ) {max (g[v], n - siz[v]);if (f[u][0 ] == siz[v]) {max (g[v], f[u][1 ]);else {max (g[v], f[u][0 ]);dfs2 (v, u);if (n - siz[u] - g[u] <= n / 2 || u == root) ans[u] = 1 ;int main () read ();for (int i = 1 ; i < n; i++) {int u = read (), v = read ();push_back (v);push_back (u);for (int i = 1 ; i <= n; i++) siz[i] = 1 ;findrt (1 , 0 );for (int i = 1 ; i <= n; i++) siz[i] = 1 ;dfs1 (root, 0 );dfs2 (root, 0 );for (int i = 1 ; i <= n; i++) {" " ;
AT_joi2015ho_b Cake 2
Link
n n n a i a_i a i A A A B B B A A A A A A
tag: 区间 DP, 环
Solution
设 f i , j f_{i, j} f i , j [ i , j ] [i, j] [ i , j ] a a a
考虑如何转移,由于两人轮流取,需要分类讨论:
当前轮 A A A [ l , r ] [l, r] [ l , r ] remain ≡ n ( m o d 2 ) \text{remain}\equiv n \pmod 2 remain ≡ n ( mod 2 ) remain \text{remain} remain A A A a l a_l a l a r a_r a r f l , r = max { f l , r − 1 + a r , f l + 1 , r + a l } f_{l, r}=\max\{f_{l, r-1}+a_r, f_{l+1, r}+a_l\} f l , r = max { f l , r − 1 + a r , f l + 1 , r + a l }
当前轮 B B B remain \text{remain} remain n n n B B B max { a l , a r } \max\{a_l, a_r\} max { a l , a r } A A A
所以有如下方程:
len ≔ l − r + 1 f l , r = { max { f l , r − 1 + a r , f l + 1 , r + a l } , len ≡ n ( m o d 2 ) f l , r − 1 , a l < a r and len ≢ n ( m o d 2 ) f l + 1 , r , a l > a r and len ≢ n ( m o d 2 ) \text{len}\coloneqq l-r+1\\
f_{l, r}=
\begin{cases}
\max\{f_{l, r-1}+a_r, f_{l+1, r}+a_l\}, &\text{len}\equiv n \pmod 2\\
f_{l, r-1}, &a_l<a_r\ \text{and}\ \text{len}\not\equiv n \pmod 2\\
f_{l+1, r}, &a_l>a_r\ \text{and}\ \text{len}\not\equiv n \pmod 2
\end{cases}
len : = l − r + 1 f l , r = ⎩ ⎨ ⎧ max { f l , r − 1 + a r , f l + 1 , r + a l } , f l , r − 1 , f l + 1 , r , len ≡ n ( mod 2 ) a l < a r and len ≡ n ( mod 2 ) a l > a r and len ≡ n ( mod 2 )
最后考虑边界,如果最后一轮是 A A A n n n i i i a i a_i a i B B B 0 0 0
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 n = read ();for (int i = 1 ; i <= n; i++) {read ();0 ] = a[n];if (n & 1 ) {for (int i = 1 ; i <= n * 2 ; i++) {for (int len = 2 ; len <= n; len++) { for (int l = 1 ; l + len - 1 <= n * 2 ; l++) {int r = l + len - 1 ;if ((len & 1 ) == (n & 1 )) { max ({f[l][r], f[l + 1 ][r] + a[l], f[l][r - 1 ] + a[r]});else { if (a[l] < a[r]) f[l][r] = max (f[l][r], f[l][r - 1 ]);else f[l][r] = max (f[l][r], f[l + 1 ][r]);int ans = 0 ;for (int i = 1 ;i <= n; i++) {max (ans, f[i][i + n - 1 ]);
P9759 [COCI2022-2023#3] Bomboni
Link
有 n × n n\times n n × n
在每个格子中写了一个数字表示此地为糖果或障碍。Iva 会吃掉所有经过的糖果(包括起点和终点的糖果)并且将糖果对应的数字相乘。Iva 知道她自己最喜欢的数字是 k k k k k k 998244353 998244353 998244353
tag: trick
Solution
考虑从因数角度分析,发现只要一条路径上覆盖了 k k k
设 f i , j , t f_{i, j, t} f i , j , t ( i , j ) (i, j) ( i , j ) k k k t t t ( i , j ) (i, j) ( i , j )
最终答案即为 f n , n , 1 f_{n, n, 1} f n , n , 1
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 f[1 ][1 ][k / __gcd(a[1 ][1 ], k)] = 1 ;for (int i = 1 ; i <= n; i++) {for (int j = 1 ; j <= n; j++) {if (i - 1 >= 1 && a[i][j] != -1 ) {for (auto x : f[i - 1 ][j]) {int nw = x.first / __gcd(x.first, a[i][j]);if (j - 1 >= 1 && a[i][j] != -1 ) {for (auto x : f[i][j - 1 ]) {int nw = x.first / __gcd(x.first, a[i][j]);
CF360B Levko and Array
Link
给定一个数列 a a a 至多 k k k
求经过修改后,max i = 2 n ∣ a i − a i − 1 ∣ \max\limits^n_{i=2}\left|a_i-a_{i-1}\right| i = 2 max n ∣ a i − a i − 1 ∣
tag: 二分, trick
Solution
注意到答案具有单调性,二分答案 x x x
考虑 check() 函数的写法,首先可以将题目中要求的最多 k k k n − k n-k n − k
不妨进行 DP,设 f i f_i f i i i i a i a_i a i ∣ a j − a i ∣ ≤ ( j − i ) × x \lvert a_j-a_i\rvert\leq (j-i)\times x ∣ a j − a i ∣ ≤ ( j − i ) × x ( i , j ) (i,j) ( i , j ) j − i + 1 j-i+1 j − i + 1 j − i j-i j − i j − i j-i j − i x x x
那么式子就很显然了:
f i = max 1 ≤ j < i { f j + 1 ∣ ∣ a j − a i ∣ ≤ ( j − i ) × x } f_i=\max_{1\leq j<i}\{f_j+1 \big| \lvert a_j-a_i\rvert\leq (j-i)\times x\}
f i = 1 ≤ j < i max { f j + 1 ∣ a j − a i ∣ ≤ ( j − i ) × x }
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 const int N = 2e3 + 10 ;const int MAXN = 2e9 ;int n, k;int a[N];int f[N];bool check (int x) for (int i = 1 ; i <= n; i++) f[i] = 1 ;for (int i = 1 ; i <= n; i++) {for (int j = 1 ; j < i; j++) {if (abs (a[i] - a[j]) <= (i - j) * x) {max (f[i], f[j] + 1 );if (f[i] >= n - k) return 1 ;return 0 ;signed main () read (); k = read ();for (int i = 1 ; i <= n; i++) {read ();int l = 0 , r = MAXN;while (l < r) {int mid = (l + r) >> 1 ;if (check (mid)) r = mid;else l = mid + 1 ;return 0 ;
P4158 [SCOI2009] 粉刷匠
Link
有 N N N M M M 0 / 1 0/1 0/1 T T T
tag: 背包
Solution
设 f i , j f_{i,j} f i , j i i i j j j
f i , j = max 1 ≤ k ≤ j { f i − 1 , j − k + g n , k } f_{i,j}=\max_{1\leq k\leq j}\{f_{i-1,j-k}+g_{n, k}\}
f i , j = 1 ≤ k ≤ j max { f i − 1 , j − k + g n , k }
其中,g i , j g_{i, j} g i , j i i i j j j
g i , j = max 0 ≤ l < i { g l , j − 1 + h l + 1 , i } g_{i,j}=\max_{0\leq l<i}\{g_{l, j-1}+h_{l+1,i}\}
g i , j = 0 ≤ l < i max { g l , j − 1 + h l + 1 , i }
其中,h l , r h_{l, r} h l , r [ l , r ] [l, r] [ l , r ] 0 0 0 1 1 1
只需要在背包的转移前维护一下 g g g h h h
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 for (int i = 1 ; i <= n; i++) {memset (g, 0 , sizeof (g));memset (maxn, 0 , sizeof (maxn));for (int l = 1 ; l <= m; l++) {for (int r = l; r <= m; r++) {int cnt0 = 0 , cnt1 = 0 ;for (int p = l; p <= r; p++) {if (s[i][p] == '0' ) cnt0++;else cnt1++;max (cnt0, cnt1);for (int j = 1 ; j <= m; j++) {for (int k = 1 ; k <= t; k++) {for (int l = 0 ; l < j; l++) {max (g[j][k], g[l][k - 1 ] + maxn[l + 1 ][j]);for (int j = t; j >= 1 ; j--) {for (int k = 1 ; k <= j; k++) {max (f[j], f[j - k] + g[m][k]);
P1156 垃圾陷阱
Link
卡门掉进深度为 D D D ≥ D \geq D ≥ D t t t h h h l l l 10 10 10 10 10 10
tag: 背包
Solution
看到两种选择,想到背包。用 f i , j f_{i, j} f i , j i i i j j j
本题与普通 0 / 1 0/1 0/1
如果选择吃掉,那么 f i , j = f i − 1 , j + l i f_{i,j}=f_{i-1,j}+l_i f i , j = f i − 1 , j + l i f i − 1 , j ≥ t i f_{i-1,j}\geq t_i f i − 1 , j ≥ t i
如果选择不吃,那么 f i , j = f i − 1 , j − h i f_{i,j}=f_{i-1,j-h_i} f i , j = f i − 1 , j − h i f i − 1 , j − h i ≥ t i ( j ≥ h i ) f_{i-1,j-h_i}\geq t_i\ (j\geq h_i) f i − 1 , j − h i ≥ t i ( j ≥ h i )
需要特判 h i > d h_i>d h i > d
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 memset (f, -INF, sizeof (f));0 ] = 10 ;read (), g = read ();for (int i = 1 ; i <= g; i++) {read (), a[i].f = read (), a[i].h = read ();max (maxn, a[i].h);sort (a + 1 , a + g + 1 );for (int i = 1 ; i <= g; i++) {for (int j = max (d, maxn); j >= 0 ; j--) {if (f[j] >= a[i].t) {max (f[j], f[j] + a[i].f);if (j >= a[i].h && f[j - a[i].h] >= a[i].t) {max (f[j], f[j - a[i].h]);if (d > maxn) {if (f[d] >= 0 ) {return 0 ;else {for (int j = d; j <= maxn; j++) {if (f[j] >= 0 ) {return 0 ;
P1772 [ZJOI2006] 物流运输
Link
物流公司要把一批货物从码头 1 1 1 n n n t t t
每日会从 1 1 1
每日有可能会有港口封锁,封锁处不可走,需要换航线并加上换航线的成本。
tag: 最短路
Solution
首先想到可以对于每一天跑一遍最短路来预处理。
考虑 DP,设 f i f_{i} f i i i i minn i , j \text{minn}_{i, j} minn i , j i i i j j j i , j i, j i , j
f i = max 1 ≤ i < j { f j + minn j + 1 , i × ( i − j ) + k } f_{i}=\max_{1\leq i<j}\{f_{j}+\text{minn}_{j+1, i}\times (i-j)+k\}
f i = 1 ≤ i < j max { f j + minn j + 1 , i × ( i − j ) + k }
另外还有前 i i i f i = minn 1 , i × i f_{i}=\text{minn}_{1,i}\times i f i = minn 1 , i × i
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 for (int i = 1 ; i <= d; i++) {read (), a = read (), b = read ();for (int j = a; j <= b; j++) {1 ;for (int i = 1 ; i <= t; i++) {for (int j = i; j <= t; j++) {reset ();for (int p = 1 ; p <= n; p++) {for (int l = i; l <= j; l++) {if (block[p][l]) {1 ;break ;dij ();for (int i = 1 ; i <= t; i++) {1 ][i] * i;for (int i = 1 ; i <= t; i++) {for (int j = 1 ; j < i; j++) {min (f[i], f[j] + minn[j + 1 ][i] * (i - j) + k);
P3174 [HAOI2009] 毛毛虫
Link
给定一颗 n n n
tag: 树形 DP, 树的直径
Solution
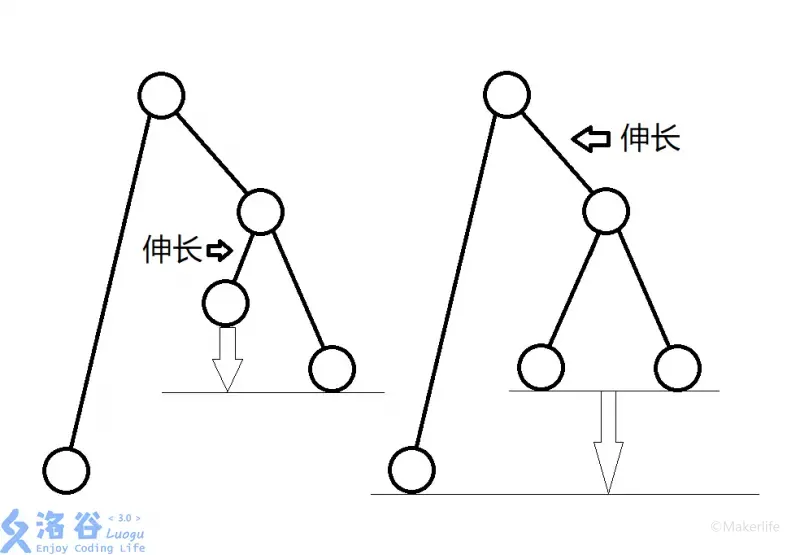
考虑从当前节点能控制的下一层节点入手,如果当前节点 u u u deg u − 1 \text{deg}_u-1 deg u − 1 deg u \text{deg}_u deg u u u u
注意需要考虑根节点没有父亲所带来的影响,和 n = 1 n=1 n = 1
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 void dfs (int u, int fa, int sum) if (sum > maxd) {for (auto v : e[u]) {if (v == fa) continue ;dfs (v, u, sum + deg[u] - 1 );int main () read (), m = read ();if (n == 1 ) {1 << endl;return 0 ;for (int i = 1 ; i <= m; i++) {int u = read (), v = read ();push_back (v);push_back (u);dfs (1 , 0 , deg[1 ] - 1 );0 ;dfs (maxpos, 0 , deg[maxpos] - 1 );2 << '\n' ;return 0 ;
P1131 [ZJOI2007] 时态同步
Link
给定一颗 n n n + 1 +1 + 1
tag: 树形 DP
Solution
要使操作次数最小,对于每个子树,就要操作根节点下的第一条边。所以从下向上递归更新答案,对于每个节点 u u u u u u
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 void dfs (int u, int fa) for (auto x : e[u]) {int v = x.v, w = x.w;if (v == fa) continue ;dfs (v, u);max (f[u], f[v] + w);for (auto x : e[u]) {int v = x.v, w = x.w;if (v == fa) continue ;
CF1324F Maximum White Subtree
Link
给定一棵 n n n u u u a u a_u a u a u a_u a u 0 0 0 u u u a u a_u a u 1 1 1 u u u
对于每个节点 u u u 包含 u u u c n t 1 cnt_1 c n t 1 c n t 2 cnt_2 c n t 2 c n t 1 − c n t 2 cnt_1 - cnt_2 c n t 1 − c n t 2
tag: 换根 DP
Solution
记 color u \text{color}_u color u u u u − 1 / 1 -1/1 − 1/1
设 f u f_u f u 1 1 1 u u u
f u = color u + ∑ v ∈ son ( u ) max { 0 , f v } f_u=\text{color}_u+\sum_{v\in \text{son}(u)}\max\{0, f_{v}\}
f u = color u + v ∈ son ( u ) ∑ max { 0 , f v }
考虑换根,设 g u g_u g u u u u u u u f u f_u f u g f a u − f u g_{fa_u}-f_u g f a u − f u f u < 0 f_u<0 f u < 0 f u f_u f u f f a u f_{fa_u} f f a u g f a u g_{fa_u} g f a u f u f_u f u
g u = f u + max { 0 , g f a u − max { 0 , f u } } g_u=f_u+\max\{0, g_{fa_u}-\max\{0, f_u\}\}
g u = f u + max { 0 , g f a u − max { 0 , f u }}
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void dfs1 (int u, int fa) for (auto v : e[u]) {if (v == fa) continue ;dfs1 (v, u);max (0 , f[v]);void dfs2 (int u, int fa) for (auto v : e[u]) {if (v == fa) continue ;max (0 , g[u] - max (0 , f[v]));dfs2 (v, u);1 ]=f[1 ]
CF607B Zuma
Link
给定一个序列,每次可删除任意长度的回文子串,最小化将序列清空的删除次数。
tag: 区间 DP
Solution
设 f l , r f_{l,r} f l , r [ l , r ] [l,r] [ l , r ]
最朴素的情况是枚举中间点,分成两部分来求,f l , r = min { f l , i + f i + 1 , r } ( i ∈ [ l , r ) ) f_{l,r}=\operatorname{min}\{f_{l,i}+f_{i+1,r}\}(i\in[l,r)) f l , r = min { f l , i + f i + 1 , r } ( i ∈ [ l , r ))
当 a l = a r a_l=a_r a l = a r
[ l + 1 , r − 1 ] [l+1,r-1] [ l + 1 , r − 1 ] [ l + 1 , r − 1 ] [l+1, r-1] [ l + 1 , r − 1 ]
所以 f l , r = min { f l , r , f l + 1 , r − 1 } ( a l = a r ) f_{l,r}=\operatorname{min}\{f_{l,r},f_{l+1,r-1}\}(a_l=a_r) f l , r = min { f l , r , f l + 1 , r − 1 } ( a l = a r )
两情况取最小值即可。
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 memset (f, INF, sizeof (f));for (int i = 1 ; i <= n; i++) {read ();1 ;for (int len = 2 ; len <= n; len++) {for (int l = 1 ; l + len - 1 <= n; l++) {int r = l + len - 1 ;if (a[l] == a[r]) {if (len == 2 ) {1 ;else {1 ][r - 1 ];for (int i = l; i < r; i++) {min (f[l][r], f[l][i] + f[i + 1 ][r]);
P1896 [SCOI2005] 互不侵犯
Link
在 N × N N \times N N × N K K K 8 8 8
tag: 状压 DP
Solution
设 f i , S , j f_{i, S, j} f i , S , j i i i S S S j j j
首先看每行的约束条件,即若 x x x x − 1 , x , x + 1 x-1, x, x+1 x − 1 , x , x + 1 S & ( S ≪ 1 ) = 0 ∧ S & ( S ≫ 1 ) = 0 S \& (S \ll 1) = 0 \land S \& (S \gg 1) = 0 S & ( S ≪ 1 ) = 0 ∧ S & ( S ≫ 1 ) = 0
其次看行与行之间的约束条件,若 x x x x − 1 , x , x + 1 x-1, x, x+1 x − 1 , x , x + 1 S S S T T T S & ( T ≪ 1 ) = 0 ∧ S & T = 0 ∧ S & ( T ≫ 1 ) = 0 S \& (T \ll 1) = 0 \land S \& T = 0 \land S \& (T \gg 1) = 0 S & ( T ≪ 1 ) = 0 ∧ S & T = 0 ∧ S & ( T ≫ 1 ) = 0
最后,容易得到转移方程:
f i , S , j = ∑ T f i − 1 , T , j − popcount ( S ) ( S & ( T ≪ 1 ) = 0 ∧ S & T = 0 ∧ S & ( T ≫ 1 ) = 0 ) f_{i, S, j} = \sum_{T} f_{i-1, T, j - \text{popcount}(S)} \quad (S \& (T \ll 1) = 0 \land S \& T = 0 \land S \& (T \gg 1) = 0)
f i , S , j = T ∑ f i − 1 , T , j − popcount ( S ) ( S & ( T ≪ 1 ) = 0 ∧ S & T = 0 ∧ S & ( T ≫ 1 ) = 0 )
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 vector<vector<vector<int >>> f (n + 10 , vector<vector<int >>((1 << n) + 10 , vector <int >(k + 10 , 0 )));0 ][0 ][0 ] = 1 ;for (int i = 1 ; i <= n; i++) {for (int j = 0 ; j < (1 << n); j++) { if ((j & (j << 1 )) || (j & (j >> 1 ))) continue ;for (int l = 0 ; l < (1 << n); l++) { if ((l & (l << 1 )) || (l & (l >> 1 ))) continue ;if ((l & j) || (l & (j >> 1 )) || (l & (j << 1 ))) continue ;for (int cnt = __builtin_popcount(j); cnt <= k; cnt++) {1 ][l][cnt - __builtin_popcount(j)];for (int i = 0 ; i < (1 << n); i++) {
P2014 [CTSC1997] 选课
Link
有 n n n s i s_i s i
一位学生要学习 m m m
tag: 树上背包
Solution
首先可以将课程关系建树。发现如果 0 0 0 0 0 0 m + 1 m+1 m + 1
设 f u , i f_{u, i} f u , i u u u i i i v v v v v v k k k
f u , i = max 0 ≤ k < i { f u , i − k + f v , k } f_{u, i}=\max_{0\leq k<i}\{f_{u, i-k}+f_{v, k}\}
f u , i = 0 ≤ k < i max { f u , i − k + f v , k }
意思是从以 u u u i − k i-k i − k v v v k k k k k k i i i
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 void dfs (int u, int m) for (auto v : e[u]) {dfs (v, m);for (int i = m; i > 0 ; i--) {for (int k = 0 ; k < i; k++) {max (f[u][i], f[u][i - k] + f[v][k]);int main () int n = read (), m = read ();for (int i = 1 ; i <= n; i++) {int k = read ();1 ] = read ();emplace_back (i);dfs (0 , m + 1 );0 ][m + 1 ] << '\n' ;
P3177 [HAOI2015] 树上染色
Link
有一棵点数为 n n n 0 ∼ n 0 \sim n 0 ∼ n k k k k k k n − k n-k n − k
tag: 树上背包
Solution
可以发现,一条边 u , v u, v u , v
contrib u , v = j × ( k − j ) + ( siz v − j ) × ( n − k − ( siz v − j ) ) \text{contrib}_{u,v}=j\times (k-j) + (\text{siz}_v-j) \times \left(n-k-\left(\text{siz}_v-j\right)\right)\\
contrib u , v = j × ( k − j ) + ( siz v − j ) × ( n − k − ( siz v − j ) )
其中,j j j v v v
设 f u , i f_{u, i} f u , i u u u i i i
f u , j = max j = max ( i − siz u + siz v ) min ( i , siz v ) ( f u , i − j + f v , j + contrib u , v × w i ) f_{u,j}=\max_{j=\max(i-\text{siz}_u+\text{siz}_v)}^{\min(i, \text{siz}_v)}\left(f_{u,i-j}+f_{v,j}+\text{contrib}_{u,v}\times w_i\right)
f u , j = j = m a x ( i − siz u + siz v ) max m i n ( i , siz v ) ( f u , i − j + f v , j + contrib u , v × w i )
这里 siz u \text{siz}_u siz u u u u 具体分析 。
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 auto dfs = [&](auto && self, int u, int fa) -> void {1 ;for (auto x : e[u]) {int v = x.v, w = x.w;if (v == fa) continue ;self (self, v, u);for (int i = min (k, siz[u]); i >= 0 ; i--) {for (int j = max (0ll , i - siz[u] + siz[v]); j <= min (i, siz[v]); j++) {int tot = j * (k - j) + (siz[v] - j) * (n - k - siz[v] + j);max (f[u][i], f[u][i - j] + f[v][j] + w * tot);
P10982 Connected Graph
Link
求 n n n n ≤ 1000 n\leq 1000 n ≤ 1000
tag: 容斥, 计数
Solution
将题意转化为求 有 n n n
n n n 2 ( n 2 ) 2^{\binom{n}{2}} 2 ( 2 n ) ( n 2 ) \binom{n}{2} ( 2 n )
考虑不连通的无向图数量。一个不连通的无向图可以分解为若干个连通块。我们可以枚举节点 1 1 1 j j j n − 1 n-1 n − 1 k − 1 k-1 k − 1 1 1 1 f i f_i f i i i i
f i = 2 ( i 2 ) − ∑ j = 1 i − 1 ( i − 1 j − 1 ) × f j × 2 ( i − j 2 ) f_i=2^{\binom{i}{2}} - \sum_{j=1}^{i-1} \binom{i-1}{j-1}\times f_j\times 2^{\binom{i-j}{2}}
f i = 2 ( 2 i ) − j = 1 ∑ i − 1 ( j − 1 i − 1 ) × f j × 2 ( 2 i − j )
Core Code
1 2 3 4 5 6 for (int i = 1 ; i <= n; i++) {ksm (2 , i * (i - 1 ) / 2 ) % mod;for (int j = 1 ; j <= i - 1 ; j++) {1 ][j - 1 ] * f[j] % mod) * ksm (2 , (i - j) * (i - j - 1 ) / 2 ) % mod + mod) % mod;