本文最后更新于 2025年3月28日 早上
由字符串全家桶入门到字符串全家桶直僵僵地镶嵌在门框里。
哈希
Hash 翻译为散列表或杂凑函数,音译为哈希,也称 Hash 表。
散列表一般由 Hash 函数和链表结构共同实现完成。
——我不知道来源。
哈希目的是把一些数据范围很大的数据(整数)或者描述保存比较复杂(字符串)利用 Hash 函数把信息映射到一个范围比较小容易维护的范围内(有点类似离散化),由于映射后的值域范围变小,有可能造成不同的原有不同信息映射为相同的值,造成冲突(映射中的多对一,一对一最理想但是有时候比较困难)。当然没有冲突是最理想的,但是关键在于 Hash 函数的选择,我们的目标是尽量减少冲突或没有冲突。
——我也不知道来源。
引入
一个简单的例子,我们要查找一个集合内的所有元素,朴素的做法是一个一个遍历,而我们通过按照每个数的个位数字分类保存,再使用链表查找,效率会更高。
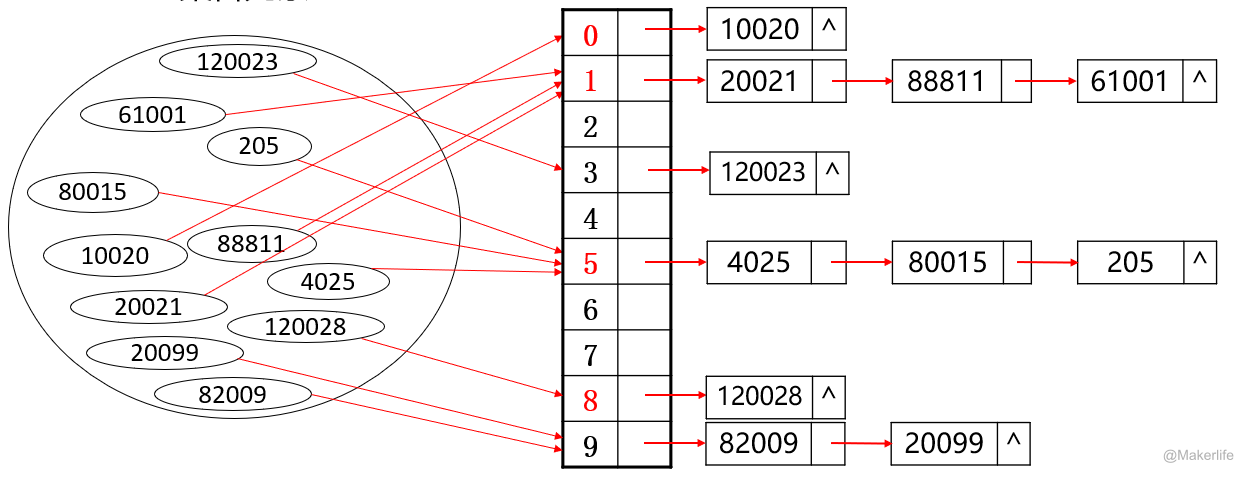
此时,按照个位数分类保存就是一个哈希函数 Hash(x)=xmod10。但是我们会发现,这种方式会发现多个数的哈希值相同,即存在很多冲突。如果 Hash(x)=xmod11,就会发现冲突少了很多。
哈希冲突的解决
解决哈希冲突两种常见的方法是闭散列和开散列。
闭散列
也叫开放地址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置(因为定义哈希表时大小肯定不能少于原始数据的个数),那么可以把 key 存放到冲突位置中的“下一个” 空位置中去。
——我还不知道来源。
寻找下一个空位置的方法一般有两种,即线性探测和二次探测。
线性探测
从哈希函数确定的位置依次向后移动 1,2,…,n 个位置,直到找到空位置为止。
二次探测
从哈希函数确定的位置依次向后移动 12,−12,22,−22,…,n 个位置,直到找到空位置为止。
当然这些不是重点,重点在后面。
开散列
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。这种方法类似图的邻接点存储,常用数组模拟。目前在实际应用中都是用这种方法。
——The Same…
其实说人话就是通过像上面 引入 部分的图一样,通过对于每个 Hash 冲突的 Hash 值建立链表。
如 A={1,5,11,15,20,21,25},哈希函数为 hash(x)=xmod10,则哈希表可用下图表示:
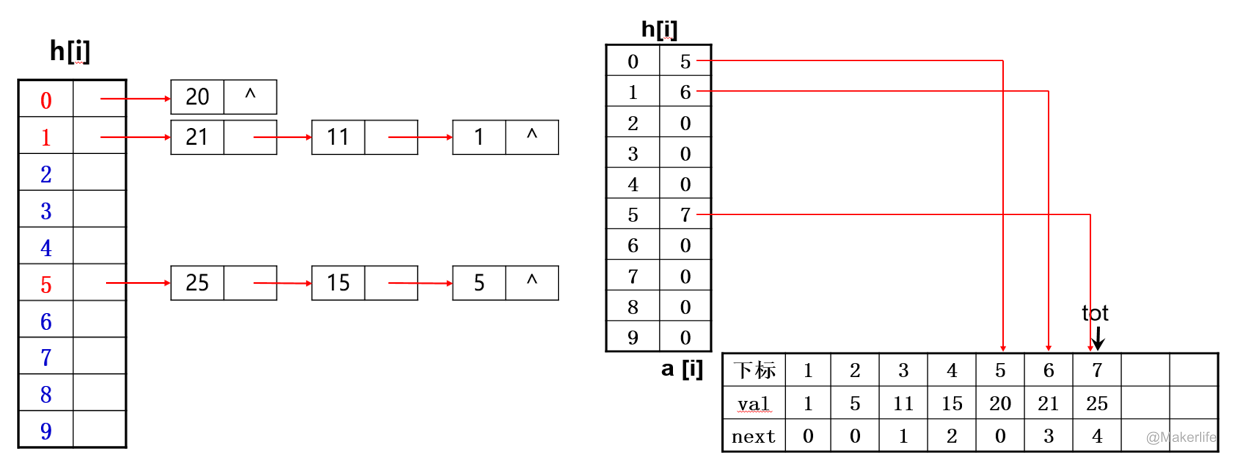
程序实现
哈希表定义
哈希表通常使用结构体定义,要分别记录哈希值、每个哈希值对应的数的个数和链表中下一个的位置,与邻接表(链式前向星)基本一致。
1
2
3
4
5
6
7
8
| const int MOD=1e6+3;
struct node{
int val;
int siz;
int nxt;
};
node e[N];
int h[MOD];
|
哈希的程序主要包含如下三个板块:哈希值计算、插入一个值、查找一个值。
哈希值的计算即为正常的取模运算。
插入函数
也与邻接表加边操作基本一致,不同之处在于如果碰到哈希值相同,应该使 sizi+1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void Insert(int x)
{
int w=x%MOD;
for(int i=h[u];i;i=e[i].nxt)
{
if(e[i].val==x)
{
e[i].siz++;
return;
}
}
e[++tot].val=x;e[tot].siz=1;
e[tot].nxt=h[u];h[u]=tot;
}
|
查找函数
遍历链表,当 vali=x 时,直接返回元素个数即 sizi,否则返回 0。
1
2
3
4
5
6
7
8
9
| inline int Find(int x)
{
int w=x%MOD;
for(int i=h[u];i;i=e[i].nxt)
{
if(e[i].val==x) return e[i].siz;
}
return 0;
}
|
例题
已知方程如下:
a1x1−a2x2+a3x3−a4x4+a5x5−a6x6=0
其中:x1,x2,…,x6 是未知数,a1,a2,…,a6 是系数,且方程中的所有数均为正整数。
求这个方程的正整数解的个数 s。
对于 100% 的数据,1≤xi≤m≤100,1≤ai≤106,s≤1015。
思路
考虑哈希。
将原式移项得:
a1x1+a3x3+a5x5=a2x2+a4x4+a6x6
通过枚举左式所有可能的情况,并将左式的结果记录在一个哈希表中,然后枚举右式的所有可能情况,查找哈希表中是否有这种情况的结果。
时间复杂度 O(m3)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| #define mod 1000007
#define int ll
const int N=1e6+10;
int m;
struct node
{
int val,siz,nxt;
}e[N];
int h[N],tot=0;
int ans=0;
int Hash(int x)
{
return x%mod;
}
void Insert(int x)
{
int w=Hash(x);
for(int i=h[w];i;i=e[i].nxt)
{
if(e[i].val==x)
{
e[i].siz++;
return ;
}
}
e[++tot].val=x;e[tot].siz++;
e[tot].nxt=h[w];h[w]=tot;
}
int Find(int x)
{
int w=Hash(x);
for(int i=h[w];i;i=e[i].nxt)
{
if(e[i].val==x) return e[i].siz;
}
return 0;
}
signed main()
{
m=read();
int a1=read(),a2=read(),a3=read(),a4=read(),a5=read(),a6=read();
for(int x1=1;x1<=m;x1++)
{
for(int x3=1;x3<=m;x3++)
{
for(int x5=1;x5<=m;x5++)
{
Insert(a1*x1+a3*x3+a5*x5);
}
}
}
for(int x2=1;x2<=m;x2++)
{
for(int x4=1;x4<=m;x4++)
{
for(int x6=1;x6<=m;x6++)
{
ans+=Find(a2*x2+a4*x4+a6*x6);
}
}
}
write(ans);el;
return 0;
}
|
还有一道板子 P3370 【模板】字符串哈希,太板了就不写了。
字符串哈希
未完待续……
Trie 树
未完待续……
KMP
KMP 算法是一种改进的字符串匹配算法,由 D.E.Knuth,J.H.Morris 和 V.R.Pratt 提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称 KMP 算法)。KMP 算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。
——Baidu Baike。
朴素的字符串匹配
设模式串 t 长度为 n,主串 s 长度为 m。
最暴力的方法显然是遍历 s,逐位匹配 t 的前缀,当前缀长度为 n 时,即为成功匹配。
复杂度显然是 O(nm)。
KMP
算法思想
考虑这样一组匹配:
前四位均匹配成功,匹配第五位时发现失配。这时,我们直接将 模式串 向右移动三位,如下所示:
此时模式串完全匹配成功。
这种算法一定是快速的,所以算法关键部分就是移动位数的计算。
Border 计算部分
Border 在 KMP 算法的定义是:字符串 s 的一个非 s 本身的子串 t,满足 t 既是 s 的前缀,又是 s 的后缀的 t 的最大长度。
设 i 为主串 s 的指针,从 1 开始遍历;j 为此时前后缀的长度。
先手算模拟大致过程,以主串为 bbacbbb 为例:
| i |
子串 |
j |
| 1 |
b |
0 |
| 2 |
b b |
1 |
| 3 |
bba |
0 |
| 4 |
bbac |
0 |
| 5 |
b bac b |
1 |
| 6 |
bb ac bb |
2 |
| 7 |
bb acb bb |
2 |
Border 数组即为所有 j。同时,不难发现,i 是后缀最后一位的下标(如果有),j 是前缀最后一位的下标。
接下来就是 Border 数组应该如何计算的问题:
我们以 i=5 为例,此时子串末尾增加了一个 b,si=s5=b,sj+1=s1=b,即此时 si=sj+1。得出结论当 si=sj+1 时,borderi=j,同时 j+1;
当 i=7 时,子串末尾增加了一个 b,根据上文的算法,bba 与 bbb 匹配失败。但此时 j 不能直接设为 0,因为整个字串的后缀还可能匹配其前缀(也就是后缀的后缀可以匹配到对应前缀)。
有一个性质 如果一个模式串的后缀匹配了一个前缀,那么这个后缀的后缀一定在这个前缀中出现了,因此对于某个等于后缀的前缀,它就出现在了这个前缀中。 即 Border 的 Border 还是 Border。
通过这个性质,我们可以发现,在这种情况下,我们可以通过将 j 跳到 borderj 上,继续向后查找。
这部分的代码,本质上是通过 s 串自己和自己匹配实现的:
1
2
3
4
5
6
7
8
9
| for(int i=2,j=0;i<=len2;i++)
{
while(j!=0 && s2[i]!=s2[j+1])
{
j=border[j];
}
if(s2[i]==s2[j+1]) j++;
border[i]=j;
}
|
匹配部分
匹配的部分与 Border 计算一样,只不过 Border 是匹配 s 的前缀和 s 后缀,而匹配则是比较 s 和 t。
代码:
1
2
3
4
5
6
7
8
9
| for(int i=1,j=0;i<=len1;i++)
{
while(j!=0 && (j==len2 || s1[i]!=s2[j+1]))
{
j=border[j];
}
if(s1[i]==s2[j+1]) j++;
if(j==len2) ans[++tot]=i-len2+1;
}
|
板子
P3375 【模板】KMP 字符串匹配
模板题,上文两部分结合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| const int N=1e6+10;
string s1,s2;
int border[N],ans[N];
int tot=0;
int main()
{
cin>>s1>>s2;
int len1=s1.size(),len2=s2.size();
s1=" "+s1;
s2=" "+s2;
for(int i=2,j=0;i<=len2;i++)
{
while(j!=0 && s2[i]!=s2[j+1])
{
j=border[j];
}
if(s2[i]==s2[j+1]) j++;
border[i]=j;
}
for(int i=1,j=0;i<=len1;i++)
{
while(j!=0 && (j==len2 || s1[i]!=s2[j+1]))
{
j=border[j];
}
if(s1[i]==s2[j+1]) j++;
if(j==len2) ans[++tot]=i-len2+1;
}
for(int i=1;i<=tot;i++)
{
write(ans[i]);el;
}
for(int i=1;i<=len2;i++)
{
write(border[i]);sp;
}
return 0;
}
|
时间复杂度
匹配时当前匹配位置每次增加 1,也就是说一共的增加量就到 n+m,跳 Border 的减少也只能减少这么多,所以就是 O(n+m)。
——zrz
参考链接
KMP字符串匹配算法 2 - Bilibili
AC 自动机
是的它不能让你直接 AC 但能让你自动 WA。
前置知识
- [Trie 字典树](#Trie 树)
- KMP
算法思想
AC 自动机其实可以理解成在字典树上运用 KMP 的思想进行字符串匹配。
KMP 是求单字符串的匹配,而 AC 自动机是求多字符串匹配一个字符串。
暴力的方法显然是有多少个字符串跑多少遍 KMP,但明显效率极低。而 AC 自动机,则是将所有的模式串构建成一颗 Trie 树。
比如模式串为 S={he,she,hers,his},则可以构建如下图的一棵 Trie 树。
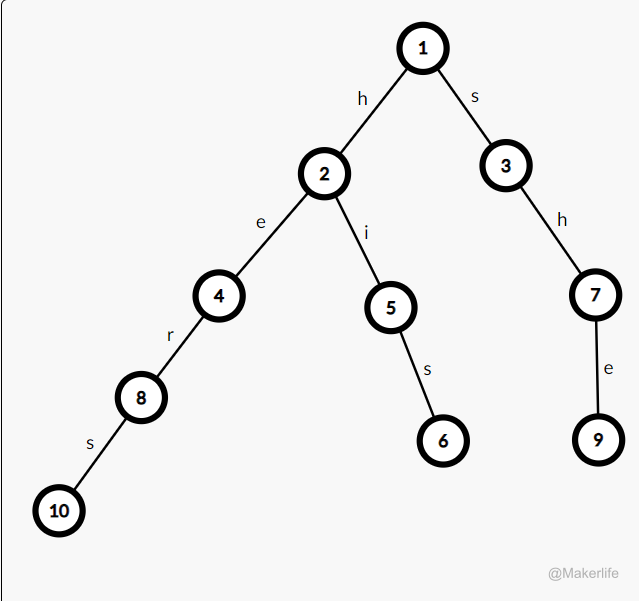
Fail 指针
如果一个模式串的后缀是任何一个模式串的前缀,则将该后缀的 Fail 指针指向该前缀。
形式化的,即若 faili=j,则 1∼j 节点的字符串是 1∼i 节点的字符串的一个后缀。
也就是说,Fail 指针是指 最长的/可以在树上找到的/当前字符串的后缀/的末尾/的下标。例如,在上图中,fail9=4。
其实看起来与 KMP 中 Border 类似,只不过 AC 自动机是查找所有模式串中的 Border。
构建 Fail
接下来看如何求 Fail。
首先可以确定的一点是,所有第二层的节点的 Fail 一定指向 root,因为没有长度比 1 还小的字符串。
另外,如果一个点的父亲的 Fail 指针(即 fafail)指向的节点有与当前点相同的字符 i,则当前点的 fail 直接指向 i,因为每次求出的 Fail 都是最长的,那最长的 Fail 加一个节点也是最长的。
而上文就表现出来一个问题,就是当求 Fail 时,需要知道当前节点父亲的 Fail,也就是说,我们需要 BFS 层次遍历来求 Fail。
我们可以建立一个 0 号节点,将其所有儿子指向 1,然后将 1 的 Fail 指向 0。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void build_fail()
{
for(int i=0;i<26;i++) t[0].c[i]=1;
queue<int> q;
q.push(1);
t[1].fail=0;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=0;i<26;i++)
{
int fafail=t[u].fail;
if(!t[u].c[i])
{
t[u].c[i]=t[fafail].c[i];
continue;
}
t[t[u].c[i]].fail=t[fafail].c[i];
q.push(t[u].c[i]);
}
}
}
|
查询 Fail
还是像 KMP 一样,如果可以匹配那就继续,如果不能匹配就跳 Fail。同时,我们可以把所有经过节点的 cnt 设为 −1,表示已经经过该节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int query(char *s)
{
int len=strlen(s+1),u=1,ans=0;
for(int i=1;i<=len;i++)
{
int now=t[u].c[s[i]-'a'];
while(now!=1 && t[now].cnt!=-1)
{
ans+=t[now].cnt;
t[now].cnt=-1;
now=t[now].fail;
}
u=t[u].c[s[i]-'a'];
}
return ans;
}
|
板子
P3808 【模板】AC 自动机(简单版)
模板题,上文两部分结合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
| #include<map>
#include<cmath>
#include<stack>
#include<queue>
#include<vector>
#include<cstdio>
#include<string>
#include<iomanip>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define mod 1000000007
#define bug(x) cout<<"Bug "<<(x)<<endl
#define el putchar('\n')
#define sp putchar(' ')
using namespace std;
inline int read()
{
int s=0,w=1;
char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0' && ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
inline void write(int x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
const int N=1e6+10;
struct node
{
int fail;
int c[26];
int cnt;
}t[N];
int tot=1;
int n;
char s[N];
void insert(char *s)
{
int len=strlen(s+1),now=1;
for(int i=1;i<=len;i++)
{
if(t[now].c[s[i]-'a']==0)
{
t[now].c[s[i]-'a']=++tot;
}
now=t[now].c[s[i]-'a'];
}
t[now].cnt++;
}
void build_fail()
{
for(int i=0;i<26;i++) t[0].c[i]=1;
queue<int> q;
q.push(1);
t[1].fail=0;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=0;i<26;i++)
{
int fafail=t[u].fail;
if(!t[u].c[i])
{
t[u].c[i]=t[fafail].c[i];
continue;
}
t[t[u].c[i]].fail=t[fafail].c[i];
q.push(t[u].c[i]);
}
}
}
int query(char *s)
{
int len=strlen(s+1),u=1,ans=0;
for(int i=1;i<=len;i++)
{
int now=t[u].c[s[i]-'a'];
while(now!=1 && t[now].cnt!=-1)
{
ans+=t[now].cnt;
t[now].cnt=-1;
now=t[now].fail;
}
u=t[u].c[s[i]-'a'];
}
return ans;
}
int main()
{
n=read();
for(int i=1;i<=n;i++)
{
scanf("%s",s+1);
insert(s);
}
build_fail();
scanf("%s",s+1);
write(query(s));el;
return 0;
}
|
参考链接
[算法]轻松掌握ac自动机 - Bilibili
题解 P3808 【【模板】AC自动机(简单版)】
Manacher
用于在 Θ(n) 的时间复杂度内寻找字符串 S 中最长回文子串的长度。
朴素算法
从 1∼n 枚举一个中间点 c,然后以此枚举最大可行的回文串长度,最后计算答案。
这样做法的时间复杂度显然是 Θ(n2) 的,并不够优秀。
Manacher 算法
过程
不难发现,在上文的定义中,回文串长度的奇偶性可能会对算法造成一定影响, 为了统一和方便计算,需要在字符串两两字符之间插入不属于 S 字符集的字符。易证此时回文子串长度(包含插入的间隔字符)长度一定为奇数。下文的回文串均默认长度为奇数。
定义一个回文串的半径 d=⌈2n⌉,左右端点下标分别为 l,r。
参照朴素算法的思路,对于每一个位置 i,我们仍需要计算极大的 di,例如,S′= #a#b#b#a 的 d 序列如下:
| i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| S′ |
~ |
# |
a |
# |
b |
# |
b |
# |
a |
# |
| d |
1 |
1 |
2 |
1 |
2 |
5 |
2 |
1 |
2 |
1 |
如果已经计算出 d,其中最大的 di−1 即为答案。
现在问题转化为如何高效地计算 d。注意到回文串具有一个极其优美的性质:若我们已知 c 是一个回文串的中心,j 也是一个回文串的中心,由于回文的对称,我们可以知道 i 也是一个合法的回文串(如图)。通过这一操作可以减少重复检查。

现在假设下一步将计算 di,而 d1∼di−1 已经被计算完成,同时维护已找到的最靠右的回文子串的边界 (lc,rc)(即具有最大 r 值的回文串,称此回文串 c 是极大的)。容易想到可以通过下面的方式实现:
- 如果 i 位于当前极大的回文串外,即 i>rc,由于 rc 右侧的字符未被检查过,只能用朴素算法求得 di;
- 若 i≤rc,就希望通过之前求得的 d 获取一些信息。由于上面的结论,似乎与 i 关于 c 对称的回文串 j 的 dj 是可以转移到 di,思路如图 xxx 所示。然而,有可能 j 区间的左端点在区间 c 外,也就是 lj<lc(如图)。此时串 j 在 lc 外的部分是否回文无法保证,正确的做法是应当尝试截断回文串,即 di 只取确定回文的长度 rc−i,然后继续用朴素算法尝试将其扩展至回文串外

时间复杂度分析
注意到每次计算时 rc 是单调不降的,且每个字符扩展比较的成本是常数。可以证明整个扫描过程中右边界最多只会被更新 Θ(n) 次,因此总体比较次数是线性的。
核心代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| n = strlen(ss+1);
s[0] = '~';
s[1] = '#';
for (int i = 1; i <= n; i++) {
s[++m] = ss[i];
s[++m] = '#';
}
maxr = 0, mid = 0, r[1] = 1;
for(int i = 2; i <= m; i++) {
if (i <= maxr) {
r[i] = min(r[mid * 2 - i], maxr - i + 1);
}
while (s[i - r[i]] == s[i + r[i]]) {
r[i]++;
}
if (i + r[i] - 1 > maxr) {
maxr = i + r[i] - 1;
mid = i;
}
}
int ans = 0;
for (int i = 1; i <= m; i++) {
ans = max(ans, r[i]);
}
cout << ans - 1 << endl;
|




