本文最后更新于 2025年11月25日 晚上
P8186 [USACO22FEB] Redistributing Gifts S
Problem Link
有一群人收到了礼物,每个人都有对每个礼物的喜爱度列表。他们商量后决定重新分配礼物,每个人都希望可以拿到他更喜爱的礼物,至少不能差于他原来的礼物。现在需要找到每个人重新分配后,他可以拿到的最喜欢的礼物是哪一个。所有人的答案可以不是同一轮中的。
tag: Floyd, 传递闭包
Solution
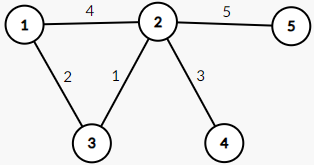
可以发现礼物的分配是由交换产生的,所以从自身向他希望得到的所有礼物连一条边。由于一开始礼物的编号和人的编号一一对应,所以连边等价于连他可以和谁交换。如果多个人 (≥ 2 \geq 2 ≥ 2
如下面的数据:
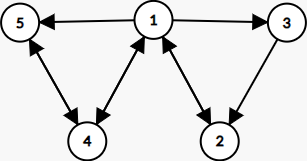
1 2 3 4 5 5 4 3 2 1
可以建出如下的图:
其中 1 2 3 与 1 5 4 均成环,有两种方案。
在图中,可以通过 Floyd 传递闭包判环,设 f i , j f_{i,j} f i , j i → j i\to j i → j f i , i = 1 f_{i,i}=1 f i , i = 1 f i , j = f i , j or ( f i , k and f k , j ) f_{i,j}=f_{i,j}\ \text{or}\ (f_{i,k}\ \text{and}\ f_{k,j}) f i , j = f i , j or ( f i , k and f k , j ) bitset 优化。
传递闭包部分代码:
1 2 3 4 5 6 7 8 bitset<N> f[N];for (int k=1 ;k<=3 ;k++) {for (int i=1 ;i<=n;i++) {for (int j=1 ;j<=n;j++) {if (f[i][j]) f[i]|=f[j];
循环 3 3 3
若 f u , v = f v , u = true f_{u,v}=f_{v,u}=\text{true} f u , v = f v , u = true u , v u, v u , v
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 bitset<N> f[N];int main () for (int i=1 ;i<=n;i++) {for (int j=1 ;j<=n;j++) {if (a[i][j-1 ]==i) break ;1 ;for (int k=1 ;k<=3 ;k++) {for (int i=1 ;i<=n;i++) {for (int j=1 ;j<=n;j++) {if (f[i][j]) f[i]|=f[j];for (int i=1 ;i<=n;i++) {for (int j=1 ;j<=n;j++) {if (f[i][a[i][j]] && f[a[i][j]][i]) {printf ("%d\n" ,a[i][j]);break ;return 0 ;
P1485 火枪打怪
Link
有 n n n m i m_i m i k k k p p p i i i p p p 左边 的怪物也可能受到溅射伤害,溅射伤害为 max ( 0 , p − ( i − j ) 2 ) \max(0, p - (i - j)^2) max ( 0 , p − ( i − j ) 2 ) p p p
tag: 二分答案, 前缀和
Solution
考虑二分答案。
注意到操作右边要比操作左边优,check 时从后往前循环。
设当前位置为 j j j i i i j j j i − j < p i-j<\sqrt{p} i − j < p [ j + 1 , j + p ] [j+1, j+\sqrt{p}] [ j + 1 , j + p ] O ( n 2 ) \mathcal{O}(n^2) O ( n 2 )
考虑优化,设区间内共操作了 s u m sum s u m r i ( 1 ≤ i ≤ s u m ) r_i(1\leq i\leq sum) r i ( 1 ≤ i ≤ s u m ) j j j
∑ i = 1 s u m [ p − ( r i , j ) 2 ] = s u m × p − ∑ i = 1 s u m r i 2 + 2 j × ∑ i = 1 s u m r i − s u m × j 2 \begin{aligned}
&\sum_{i=1}^{sum}[p-(r_i, j)^2]\\
=&sum\times p-\sum_{i=1}^{sum}r_i^2+2j\times \sum_{i=1}^{sum}r_i-sum\times j^2
\end{aligned}
= i = 1 ∑ s u m [ p − ( r i , j ) 2 ] s u m × p − i = 1 ∑ s u m r i 2 + 2 j × i = 1 ∑ s u m r i − s u m × j 2
这样的复杂度仍为 O ( n 2 ) \mathcal{O}(n^2) O ( n 2 ) s u m sum s u m s u m j ′ sum^{\prime}_j s u m j ′ j ∼ n j\sim n j ∼ n r j r_j r j r j 2 r_j^2 r j 2 r j ′ r^{\prime}_j r j ′ j ∼ n j\sim n j ∼ n r j ′ 2 r^{\prime 2}_j r j ′2 O ( n ) \mathcal{O}(n) O ( n )
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 bool check (int p) int maxd = sqrt (p);for (int i = 1 ; i <= n; i++) {for (int j = n; j >= 1 ; j--) {1 ];1 ];1 ];int nowsum = sum[j] - sum[j + maxd + 1 ];1 ])2 * j * (ri[j] - ri[j + maxd + 1 ])while (hp[j] >= 0 ) {if (sum[j] > k) return 0 ;return 1 ;
P6600 「EZEC-2」字母
Link
在 0 / 1 0/1 0/1 w w w h h h
w ≥ a w\geq a w ≥ a h ≥ b h\geq b h ≥ b w × h ≥ s w\times h\geq s w × h ≥ s w + h ≥ x w+h\geq x w + h ≥ x
tag: 二维前缀和
Solution
一眼非常像 NOIP2022 T1。
首先想如何 brute,先枚举矩阵中每个为 1 1 1 1 1 1 s u m l , s u m r , s u m d suml, sumr, sumd s u m l , s u m r , s u m d 1 1 1
考虑优化掉判断符合条件部分的算法,暴力枚举横长竖长,f w , h f_{w, h} f w , h w w w h h h O ( n 2 ) \mathcal{O}(n^2) O ( n 2 )
计算答案时,对于每个位置 ( i , j ) (i,j) ( i , j ) w m a x = min { s u m l i , j , s u m r i , j } × 2 − 1 , h m a x = s u m d i , j w_{max} = \min\{suml_{i, j}, sumr_{i, j}\}\times 2 - 1,\ h_{max} = sumd_{i, j} w ma x = min { s u m l i , j , s u m r i , j } × 2 − 1 , h ma x = s u m d i , j a n s i , j = ∑ w = 3 w m a x ∑ h = 2 h m a x f w , h ans_{i, j} = \sum_{w = 3}^{w_{max}}\sum_{h = 2}^{h_{max}} f_{w, h} an s i , j = ∑ w = 3 w ma x ∑ h = 2 h ma x f w , h
继续优化掉这一部分,注意到是统计区间和,想到二维前缀和,用 s u m i , j sum_{i, j} s u m i , j ∑ w = 3 i ∑ h = 2 j f w , h \sum_{w = 3}^{i}\sum_{h = 2}^{j} f_{w, h} ∑ w = 3 i ∑ h = 2 j f w , h s u m i , j = s u m i − 1 , j + s u m i , j − 1 + f i , j − s u m i − 1 , j − 1 sum_{i, j} = sum_{i - 1, j} + sum_{i, j - 1} + f_{i, j} - sum_{i - 1, j - 1} s u m i , j = s u m i − 1 , j + s u m i , j − 1 + f i , j − s u m i − 1 , j − 1
这样总体复杂度 O ( n 2 ) \mathcal{O}(n^2) O ( n 2 )
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 for (int i = 1 ; i <= n; i++) {for (int j = 1 ; j <= m; j++) {if (in[i][j] == '0' ) suml[i][j] = 0 ;else suml[i][j] = suml[i][j - 1 ] + 1 ;for (int j = m; j >= 1 ; j--) {if (in[i][j] == '0' ) sumr[i][j] = 0 ;else sumr[i][j] = sumr[i][j + 1 ] + 1 ;for (int j = 1 ; j <= m; j++) {for (int i = n; i >= 1 ; i--) {if (in[i][j] == '0' ) sumd[i][j] = 0 ;else sumd[i][j] = sumd[i + 1 ][j] + 1 ;for (int w = 3 ; w <= m; w++) {for (int h = 2 ; h <= n; h++) {if ((w & 1 ) && w >= a && h >= b && w * h >= s && w + h >= x) {1 ;1 ][h] + sum[w][h - 1 ] + f[w][h] - sum[w - 1 ][h - 1 ];int ans = 0 ;for (int i = 1 ; i <= n; i++) {for (int j = 1 ; j <= m; j++) {int w = min (suml[i][j], sumr[i][j]) * 2 - 1 ;int h = sumd[i][j];if (in[i][j] == '1' ) ans += sum[w][h];
P7915 [CSP-S 2021] 回文
Link
给定一个整数序列 a 1 , a 2 , … , a 2 n a_1, a_2,\dots, a_{2n} a 1 , a 2 , … , a 2 n 1 ∼ n 1\sim n 1 ∼ n a a a b b b a a a b b b L 或 R,表示从开头或结尾选择元素,输出操作串字典序最小的方案。
tag: 双端队列
Solution
以下以第一步取 a 1 a_1 a 1 a 2 n a_{2n} a 2 n
由于要构成回文串,对于有且仅有的一个 k k k a 1 = a k a_1=a_k a 1 = a k a k a_k a k
所以题目可以转化为,对于 a 2 … a k − 1 a_2\dots a_{k-1} a 2 … a k − 1 a k + 1 … a 2 n a_{k+1}\dots a_{2n} a k + 1 … a 2 n
即可以把这两部分看作一个栈,从第二次操作开始,每次从栈顶取元素,那么应该从哪边取呢?
可以从最后的操作开始分析,倒数第二次操作只能取 a k − 1 a_{k-1} a k − 1 a k + 1 a_{k+1} a k + 1 a k a_k a k
一个 string 需要注意的点,每次 s = "L" + s 的复杂度是 O ( n ) \mathcal{O}(n) O ( n ) s.push_back("L") 最后 reverse(s.begin(), s.end()) 来解决。
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 bool check_l () int k;"L" ;"L" ;for (int i = 2 ; i <= n; i++) {if (a[i] == a[1 ]) {break ;int > st1, st2;for (int i = 2 ; i < k; i++) st1. push_back (a[i]);for (int i = k + 1 ; i <= n; i++) st2. push_front (a[i]);while (!st1. empty () || !st2. empty ()) {if (st1. size () > 1 && st1.f ront() == st1. back ()) {push_back ('L' );push_back ('L' );1. pop_front (); st1. pop_back ();else if (st1. size () && st2. size () && st1.f ront() == st2. back ()) {push_back ('L' );push_back ('R' );1. pop_front (); st2. pop_back ();else if (st1. size () && st2. size () && st2.f ront() == st1. back ()) {push_back ('R' );push_back ('L' );2. pop_front (); st1. pop_back ();else if (st2. size () > 1 && st2.f ront() == st2. back ()) {push_back ('R' );push_back ('R' );2. pop_front (); st2. pop_back ();else {return 0 ;return 1 ;bool check_r () int k;"R" ;"L" ;for (int i = 1 ; i < n; i++) {if (a[i] == a[n]) {break ;int > st1, st2;for (int i = 1 ; i < k; i++) st1. push_back (a[i]);for (int i = k + 1 ; i < n; i++) st2. push_front (a[i]);while (!st1. empty () || !st2. empty ()) {if (st1. size () > 1 && st1.f ront() == st1. back ()) {push_back ('L' );push_back ('L' );1. pop_front (); st1. pop_back ();else if (st1. size () && st2. size () && st1.f ront() == st2. back ()) {push_back ('L' );push_back ('R' );1. pop_front (); st2. pop_back ();else if (st1. size () && st2. size () && st2.f ront() == st1. back ()) {push_back ('R' );push_back ('L' );2. pop_front (); st1. pop_back ();else if (st2. size () > 1 && st2.f ront() == st2. back ()) {push_back ('R' );push_back ('R' );2. pop_front (); st2. pop_back ();else {return 0 ;return 1 ;int main () read ();while (T--) {read () * 2 ;for (int i = 1 ; i <= n; i++) {read ();if (check_l ()) {reverse (revans.begin (), revans.end ());else if (check_r ()) {reverse (revans.begin (), revans.end ());else {-1 << endl;return 0 ;
P1053 [NOIP2005 提高组] 篝火晚会
Link
佳佳刚进高中,在军训的时候,由于佳佳吃苦耐劳,很快得到了教官的赏识,成为了“小教官”。在军训结束的那天晚上,佳佳被命令组织同学们进行篝火晚会。一共有 n ( 3 ≤ n ≤ 50000 ) n(3\le n \le 50000) n ( 3 ≤ n ≤ 50000 ) 1 1 1 n n n 1 , 2 , ⋯ , n 1,2,\cdots ,n 1 , 2 , ⋯ , n
佳佳可向同学们下达命令,每一个命令的形式如下:
( b 1 , b 2 , . . . b m − 1 , b m ) (b_1, b_2,... b_{m-1}, b_m) ( b 1 , b 2 , ... b m − 1 , b m )
这里 m m m m m m b 1 , b 2 , ⋯ , b m b_1,b_2,\cdots, b_m b 1 , b 2 , ⋯ , b m m m m b 1 b_1 b 1 b 2 b_2 b 2 b 2 b_2 b 2 b 3 b_3 b 3 b m b_m b m b 1 b_1 b 1 m m m m m m
选择的 m m m
tag: 环
Solution
发现如果有 k k k n − k n-k n − k
但是建出来的环不一定能使 k k k
初始环
1
2
3
4
5
6
目标环
2
3
4
5
6
1
差值
1
1
1
1
1
1
注意到相同差值的位置可以通过旋转变成 0 0 0 k m a x k_{max} k ma x n − k m a x n-k_{max} n − k ma x
考虑如何构造目标环,首先设 l i , r i l_i, r_i l i , r i i i i a n = l 1 , a 1 = 1 a_n=l_1, a_1=1 a n = l 1 , a 1 = 1 i i i n n n
注意计算差值时,不能直接 a i − i a_i-i a i − i n n n m o d n \bmod{n} mod n
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 for (int i = 1 ; i <= n; i++) {if ((i != l[ l[i] ] && i != r[ l[i] ]) || (i != l[ r[i] ] && i != r[ r[i] ])) {-1 << endl;return 0 ;push_back (0 );push_back (1 );a.push_back (l[1 ]);1 ] = vis[l[1 ]] = 1 ;int now = l[1 ];while (a.size () != n + 1 ) {if (!vis[ l[now] ]) {push_back (l[now]);1 ;else if (!vis[ r[now] ]) {push_back (r[now]);1 ;int maxn = 0 ;for (int i = 1 ; i <= n; i++) {for (int i = 0 ; i < n; i++) {max (maxn, t[i]);for (int i = 0 ; i <= n; i++) t[i] = 0 ;for (int i = 1 ; i <= n; i++) {1 )) % n]++;for (int i = 0 ; i < n; i++) {max (maxn, t[i]);
AT_joi2015ho_c JOI Park
Link
时值 20 XX 20\text{XX} 20 XX N N N 1 1 1 N N N M M M 1 1 1 M M M i ( 1 ≤ i ≤ M ) i(1 \leq i \leq M) i ( 1 ≤ i ≤ M ) A i A_i A i B i B_i B i D i D_i D i
修缮计划如下:首先,选择一个自然数 X X X X X X X X X i i i j j j i i i j j j C C C C C C C × X C\times X C × X
接下来,撤去已经通过地下通道连接的广场之间的道路。撤去道路的花费不计。
最后,将没有被撤去的道路进行修补,长为 d d d d d d
修缮计划实施之前,JOI 公园没有地下通道。请求出 JOI 公园修缮花费总和的最小值。
需要注意的是删除的道路不只是 1 → u 1\to u 1 → u 1 → u → v ( d i s u < d i s v ) 1\to u\to v(dis_u<dis_v) 1 → u → v ( d i s u < d i s v )
tag: 最短路
Solution
首先注意到选择的 X X X u u u 1 1 1 d i s u dis_u d i s u d i s u dis_u d i s u 1 , 3 , 2 , 4 , 5 1, 3, 2, 4, 5 1 , 3 , 2 , 4 , 5
一个例子,计算完 2 2 2 1 → 2 1\to 2 1 → 2 3 3 3 1 → 3 1\to 3 1 → 3 2 → 3 2\to 3 2 → 3
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #define int ll int n, m, c;struct node {int pos, dis;bool operator <(const node& x) const {return dis > x.dis;struct edge {int v, w;int sum = 0ll ;void dij (int u) for (int i = 1 ; i <= n; i++) {1 ].dis = 0ll ;push ({1 , 0 });while (!q.empty ()) {int u = q.top ().pos;pop ();if (vis[u]) continue ;1ll ;for (auto x : e[u]) {int v = x.v, w = x.w;if (dis[v].dis > dis[u].dis + w) {if (!vis[v]) q.push ({v, dis[v].dis});signed main () read (); m = read (); c = read ();for (int i = 1 ; i <= m; i++) {int u = read (), v = read (), w = read ();push_back ({v, w});push_back ({u, w});for (int i = 1 ; i <= n; i++) {dij (1 );sort (dis + 1 , dis + n + 1 );int minn = INF;int last = 0 ;reset ();for (int i = n; i >= 1 ; i--) {int ans = dis[i].dis * c;1 ;for (auto x : e[dis[i].pos]) {int v = x.v, w = x.w;if (vis[v]) last += w;min (minn, ans - last);return 0 ;
AGC001C Shorten Diameter
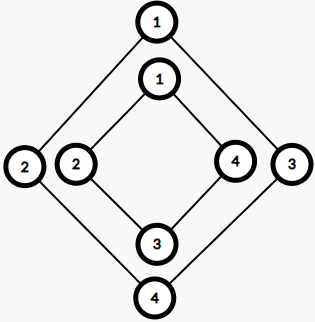
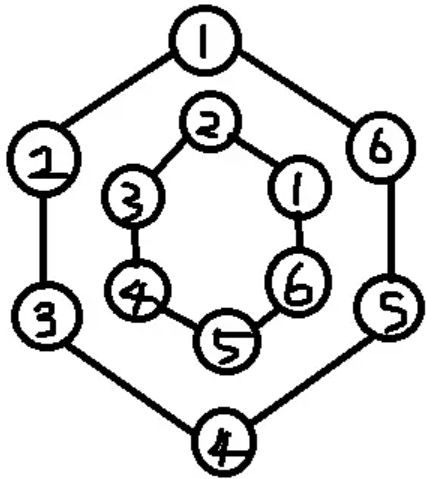
给定一颗 n n n k k k
tag: 树的直径
Solution
将题目转化为寻找一个中心,使中心左右两边最多延伸 k 2 \dfrac{k}{2} 2 k t o t tot t o t n − t o t n-tot n − t o t
如果 k k k
如果 k k k
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 int tot;void dfs (int u, int fa, int step) if (step == 0 ) return ;for (auto v : e[u]) {if (v == fa) continue ;dfs (v, u, step - 1 );int main () int ans = INF;if (!(k & 1 )) {for (int i = 1 ; i <= n; i++) {0 ;dfs (i, 0 , k / 2 );min (ans, n - tot);else {for (int u = 1 ; u <= n; u++) {for (auto v : e[u]) {0 ;dfs (v, u, k / 2 );dfs (u, v, k / 2 );min (ans, n - tot);
P8677 [蓝桥杯 2018 国 A] 采油
Link
tag: 贪心
Solution
第一问显然最优情况下答案为边权和的两倍。
考虑第二问,对于一个点 u u u S u S_u S u
首先认为 B u ≥ S u B_u\geq S_u B u ≥ S u B u < S u B_u<S_u B u < S u S u S_u S u
若只有一个节点,那么耗费的人显然为 B u B_u B u
若有两个节点,不妨设为 x x x y y y B x − S x > B y − S y B_x-S_x>B_y-S_y B x − S x > B y − S y x x x y y y x x x x x x y y y max { B x , B x + B y − ( B x − S x ) } = max { B x , B y + S x } \max\{B_x, B_x+B_y-(B_x-S_x)\}=\max\{B_x, B_y+S_x\} max { B x , B x + B y − ( B x − S x )} = max { B x , B y + S x } y y y x x x max { B y , B x + S y } \max\{B_y, B_x+S_y\} max { B y , B x + S y } B y + S x < B x + S y B_y+S_x<B_x+S_y B y + S x < B x + S y
将结论推广到同一层上有 k k k
再考虑更一般的情况,在满足第一问的限制下,即按照最短路径,一定是先遍历完每个子树最短。所以搜到一个点时,先将这个点为根的所有子树缩点,按照剩余人数排序,递归继续缩点。
注意搜索时需要从 B − S B-S B − S
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 struct node {int b, s;bool operator <(const node &x) const {return b - s > x.b - x.s;operator +(const node &x) const {max (b, s + x.b), res.s = s + x.s;return res;node dfs (int u, int fa) {push_back (a[u]);for (auto v : e[u]) {if (v == fa) continue ;push_back (dfs (v, u));0 ;sort (p.begin (), p.end ());for (auto v : p) res = res + v;return res;int main () read ();int sum = 0 ;int maxn = 0 , maxpos = 1 ;for (int i = 1 ; i <= n; i++) {read ();for (int i = 1 ; i <= n; i++) {read ();max (a[i].b, a[i].s);if (a[i].b - a[i].s > maxn) {for (int i = 1 ; i < n; i++) {int v = read (), w = read ();1 ].push_back (v);push_back (i + 1 );2 << " " << dfs (maxpos, 0 ).b << '\n' ;return 0 ;
P2659 美丽的序列
Link
给定一个序列,找到一个区间使得区间最小值与区间长度的乘积最大,输出乘积。
tag: 单调栈
Solution
维护区间最小值,想到用单调栈。
单调递增栈,当遍历后面的元素时,如果此时元素比之前元素最小值小,那么之前元素的最小值地位从当前元素开始失效,也就可以得到之前元素所管辖的区间右端点。同理,也可以找到当前元素管辖区间的左端点,即为弹栈后的栈顶,也就是前面第一个大于当前元素的位置。
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 for (int i = 1 ; i <= n; i++) {1 , q[i].r = n;while (!st.empty () && a[st.top ()] > a[i]) {top ()].r = i - 1 ;pop ();if (!st.empty ()) q[i].l = st.top () + 1 ;push (i);int ans = 0 ;for (int i = 1 ; i <= n; i++) {max (ans, (q[i].r - q[i].l + 1 ) * a[i]);
P12177 [蓝桥杯 2025 省 Python B] 异或和
Link
求:
∑ i = 1 n ∑ j = i + 1 n ( a i ⊕ a j ) × ( j − i ) \sum_{i=1}^{n} \sum_{j=i+1}^{n} (a_i \oplus a_j) \times (j - i)
i = 1 ∑ n j = i + 1 ∑ n ( a i ⊕ a j ) × ( j − i )
tag: 二进制按位
Solution
按位考虑,注意到为 1 ⊕ 0 = 1 1\oplus0=1 1 ⊕ 0 = 1
按位枚举,对于每一位的数正向扫,统计之前有多少个数可以产生贡献 n u m num n u m l s u m lsum l s u m
当前枚举到第 j j j
如果当前位为 0 0 0 2 i × ( j × n u m − l s u m ) 2^i\times (j\times num - lsum) 2 i × ( j × n u m − l s u m )
如果为 1 1 1 1 1 1
时间复杂度 O ( n log n ) \mathcal{O}(n\log n) O ( n log n )
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 for (int i = 0 ; i <= 20 ; i++) {int lsum = 0 , num = 0 ;for (int j = 1 ; j <= n; j++) {int v = ((a[j] >> i) & 1 );if (!v) {1 << i) * (num * j - lsum);else {1 << i) * ((j - 1 - num) * j - ((j - 1 ) * j / 2 - lsum));
P3831 [SHOI2012] 回家的路
Link
有一个 n × n n\times n n × n
换乘花费为 1 1 1 2 2 2
tag:分层图, 最短路
Solution
考虑将起点、终点和可换乘的格点作为节点,对两两直接可达的节点连边。
显然同一行或同一列内相邻两换乘站应当连边,想到分层图。
所有行为一层、所有列为一层建图。同时,上下两层对应相同的节点连边权为 1 1 1
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 bool cmpx (node a, node b) if (a.x != b.x) return a.x < b.x;else return a.y < b.y;bool cmpy (node a, node b) if (a.y != b.y) return a.y < b.y;else return a.x < b.x;int main () read (), n = read ();for (int i = 1 ; i <= n; i++) {int x = read (), y = read ();push_back ({i + n + 2 , 1 });2 ].push_back ({i, 1 });0 ].x = read (), p[0 ].y = read (), p[0 ].id = 0 ;1 ].x = read (), p[n + 1 ].y = read (), p[n + 1 ].id = n + 1 ;sort (p, p + n + 2 , cmpy);for (int i = 0 ; i <= n; i++) {if (p[i].y == p[i + 1 ].y) {int dis = abs (p[i].x - p[i + 1 ].x);push_back ({p[i + 1 ].id, 2 * dis});1 ].id].push_back ({p[i].id, 2 * dis});sort (p, p + n + 2 , cmpx);for (int i = 0 ; i <= n; i++) {if (p[i].x == p[i + 1 ].x) {int dis = abs (p[i].y - p[i + 1 ].y);2 ].push_back ({p[i + 1 ].id + n + 2 , 2 * dis});1 ].id + n + 2 ].push_back ({p[i].id + n + 2 , 2 * dis});int ans = INF;0 ;dij ();min ({w.dis[n + 1 ], w.dis[n + 1 + n + 2 ]});2 ;reset ();dij ();min ({ans, w.dis[n + 1 ], w.dis[n + 1 + n + 2 ]});
P3594 [POI 2015 R3] 狼坑 Trous de loup
Link
给定一个长度为 n n n d d d 0 0 0 p p p
tag: 双指针, 单调队列
Solution
首先容易得到,选择的区间长度一定为 d d d
考虑暴力,枚举左右端点和选择的区间,时间复杂度 O ( n 3 ) \mathcal{O}(n^3) O ( n 3 )
考虑优化,不难想到双指针,可以把暴力的枚举左右端点部分优化掉,时间复杂度 O ( n 2 ) \mathcal{O}(n^2) O ( n 2 )
观察最终答案的式子:
max l , r ( r − l + 1 ) s.t. ∑ i = l r w i − max k ∈ [ l , r − d + 1 ] ∑ j = k k + d − 1 w j ≤ p \max_{l, r} \left(r - l + 1\right)\quad \text{s.t.} \quad\sum_{i=l}^r w_i - \max_{k\in \left[l, r - d + 1\right]}\sum_{j=k}^{k+d-1} w_j \leq p
l , r max ( r − l + 1 ) s.t. i = l ∑ r w i − k ∈ [ l , r − d + 1 ] max j = k ∑ k + d − 1 w j ≤ p
注意到复杂度瓶颈在于 max k ∈ [ l , r − d + 1 ] ∑ j = k k + d − 1 w j \max_{k\in \left[l, r - d + 1\right]}\sum_{j=k}^{k+d-1} w_j max k ∈ [ l , r − d + 1 ] ∑ j = k k + d − 1 w j
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 deque<int > q; emplace_back (d);int ans = d;for (int r = d + 1 ; r <= n; r++) {while (!q.empty () &&back ()] - sum[q.back ()-d] <= sum[r] - sum[r-d]) {pop_back ();emplace_back (r);while (!q.empty () && q.front () - d + 1 < l) q.pop_front ();while (!q.empty () && sum[r] - sum[l-1 ] - (sum[q.front ()] - sum[q.front ()-d]) > p) {while (!q.empty () && q.front () - d + 1 < l) q.pop_front ();max (ans, r - l + 1 );
P10957 环路运输
Link
在一条环形公路旁均匀地分布着 N N N 1 ∼ N 1 \sim N 1 ∼ N i i i j j j d i s t ( i , j ) = min ( ∣ i − j ∣ , N − ∣ i − j ∣ ) dist(i,j)=\min(|i-j|,N-|i-j|) d i s t ( i , j ) = min ( ∣ i − j ∣ , N − ∣ i − j ∣ ) i i i j j j a i a_i a i
在 i i i j j j a i + a j + d i s t ( i , j ) a_i+a_j+dist(i,j) a i + a j + d i s t ( i , j )
tag: 单调队列
Solution
首先断环为链,考虑化简最终答案的式子:
f i , j = a i + a j + min ( ∣ i − j ∣ , n − ∣ i − j ∣ ) ( 1 ≤ j < i ≤ n ) = a i + a j + ( i − j ) ( 1 ≤ j < i ≤ 2 n , i − j < ⌊ n 2 ⌋ ) ans = max 1 ≤ j < i ≤ 2 n f i , j = max 1 ≤ j < i ≤ 2 n , i − j < ⌊ n 2 ⌋ ( a i + i ) + ( a j − j ) . \begin{aligned}
f_{i,j}
&= a_i + a_j + \min\!\left( |i-j|,\; n - |i-j| \right) &&\left(1 \leq j < i \leq n\right) \\
&= a_i + a_j + (i-j) &&\left(1 \leq j < i \leq 2n,\; i-j < \left\lfloor \frac{n}{2} \right\rfloor \right)\\
\text{ans}
&= \max_{1 \leq j < i \leq 2n} f_{i,j} \\
&= \max_{1 \leq j < i \leq 2n, i-j < \left\lfloor \frac{n}{2} \right\rfloor} \left(a_i + i \right) + \left(a_j - j \right).
\end{aligned}
f i , j ans = a i + a j + min ( ∣ i − j ∣ , n − ∣ i − j ∣ ) = a i + a j + ( i − j ) = 1 ≤ j < i ≤ 2 n max f i , j = 1 ≤ j < i ≤ 2 n , i − j < ⌊ 2 n ⌋ max ( a i + i ) + ( a j − j ) . ( 1 ≤ j < i ≤ n ) ( 1 ≤ j < i ≤ 2 n , i − j < ⌊ 2 n ⌋ )
注意到 ( a i + i ) (a_i + i) ( a i + i ) j j j i i i [ i − ⌊ n 2 ⌋ , i − 1 ] \left[i - \left\lfloor\dfrac{n}{2}\right\rfloor, i - 1\right] [ i − ⌊ 2 n ⌋ , i − 1 ] a j − j a_j - j a j − j
Core Code
1 2 3 4 5 6 7 8 9 10 for (int i = 1 ; i <= 2 * n; i++) {while (!q.empty () && i - q.front () > n / 2 ) {pop_front ();if (!q.empty ()) ans = max (ans, a[q.front ()] - q.front () + a[i] + i);while (!q.empty () && a[q.back ()] - q.back () <= a[i] - i) {pop_back ();push_back (i);
P1948 [USACO08JAN] Telephone Lines S
Link
给定一个简单无向图,有边权。最小化 1 → n 1\to n 1 → n k + 1 k + 1 k + 1
tag: 二分答案, 最短路
Solution
二分答案枚举答案 mid \text{mid} mid mid \text{mid} mid 1 1 1 0 0 0 1 → n 1\to n 1 → n k k k
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 auto check = [&](int mid) -> bool {int > dis (n + 1 , numeric_limits<int >::max () / 2 );vector<char > vis (n + 1 ) ;1 ] = 0 ;push (Node{1 , 0 });while (!q.empty ()) {int u = q.top ().pos;pop ();if (vis[u]) continue ;1 ;for (auto x : e[u]) {int v = x.v, w = x.w;if (w > mid) w = 1 ;else w = 0 ;if (dis[v] > dis[u] + w) {if (!vis[v]) q.push (Node{v, dis[v]});if (dis[n] <= k) return true ;else return false ;int l = 0 , r = MAXN;while (l < r) {int mid = (l + r) >> 1 ;if (check (mid)) r = mid;else l = mid + 1 ;
P10454 奇数码问题
Link
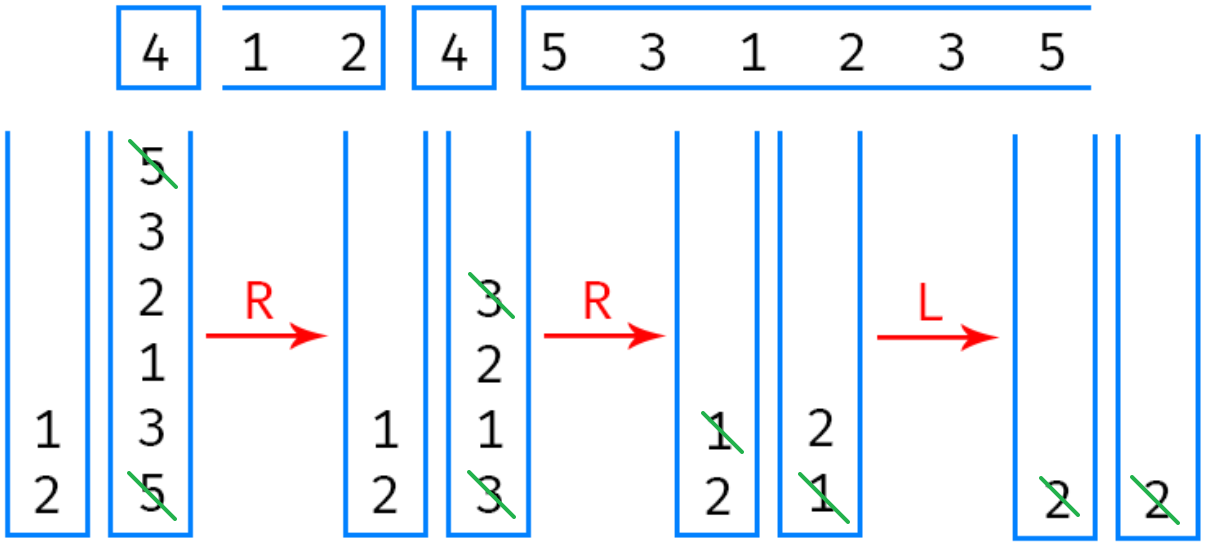
给定一个初始矩阵和一个目标矩阵。其中的 0 可以与其四联通的块交换位置。通过若干次操作,判断是否能从初始矩阵变为目标矩阵。
tag: 逆序对
Solution
考虑将矩阵按行展开为一维数组,忽略 0。
考虑两种操作:上下移动和左右移动。
左右移动:注意到元素在忽略 0 后相对顺序不变,所以不会改变逆序对数量的奇偶性;
上下移动:考虑一个元素 x x x 1 2 3 5 2 8 5 _ 8 1 _ 3 1 2 3 4 6 7 4 6 7
n − 1 n-1 n − 1 n n n
所以,两矩阵可互相转化和充要条件是两序列的逆序对数量奇偶性相同。
P2512 [HAOI2008] 糖果传递
有 n n n a i a_i a i 1 1 1
tag: 贪心, 推式子
Solution
我们设每人最终糖果数为 x ˉ \bar x x ˉ x i x_i x i
{ a i + x i + 1 − x i = x ˉ , 1 ≤ i < n a n + x 1 − x n = x ˉ , i = n \begin{cases}
a_i+x_{i+1}-x_i &= \bar x ,&& 1\leq i< n\\
a_n+x_1-x_n &= \bar x ,&& i=n\\
\end{cases}
{ a i + x i + 1 − x i a n + x 1 − x n = x ˉ , = x ˉ , 1 ≤ i < n i = n
对 1 ≤ i < n 1\leq i<n 1 ≤ i < n
x i + 1 = x ˉ + x i − a i x_{i+1} = \bar x+x_i-a_i
x i + 1 = x ˉ + x i − a i
将 x = i + 1 x=i+1 x = i + 1 x = i + 2 x=i+2 x = i + 2
x n = ( n − 1 ) x ˉ + x 1 − ∑ i = 1 n − 1 a i x_n = (n-1)\bar x+x_1-\sum_{i=1}^{n-1}a_i
x n = ( n − 1 ) x ˉ + x 1 − i = 1 ∑ n − 1 a i
设 c i = ∑ j = 1 i a j − i x ˉ c_i=\sum_{j=1}^{i} a_j-i\bar x c i = ∑ j = 1 i a j − i x ˉ
x i = x 1 − c i x_i=x_1-c_i
x i = x 1 − c i
题目要求最小化 ∑ i = 1 n ∣ x i ∣ \sum_{i=1}^{n} |x_i| ∑ i = 1 n ∣ x i ∣ ∑ i = 1 n ∣ x 1 − c i ∣ \sum_{i=1}^{n} |x_1-c_i| ∑ i = 1 n ∣ x 1 − c i ∣ ∑ i = 1 n ∣ x 1 − c i ∣ \sum_{i=1}^{n} |x_1-c_i| ∑ i = 1 n ∣ x 1 − c i ∣ x 1 x_1 x 1 x 1 x_1 x 1 c i c_i c i
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 vector<int > sum (n + 1 ) ;for (int i = 1 ; i <= n; i++) {int a = read ();1 ] + a;for (int i = 1 ; i <= n; i++) {sort (c.begin () + 1 , c.begin () + n + 1 );int ans = 0 ;int mid = c[(n + 1 ) >> 1 ];for (int i = 1 ; i <= n; i++) {abs (mid - c[i]);
P14401 [JOISC 2016] 电报 / Telegraph
Link
有一个 n n n 1 1 1 n n n A i A_i A i C i C_i C i
tag: 贪心
Solution
首先题意可以转化为最小代价使得图变为包含所有 n n n
考虑证明这一点:若存在一点 u u u u u u
将总代价转化为 ∑ C i \sum C_i ∑ C i
我们想保留一些原始边,并添加一些新边(修改后的边)将他们连成一个大环,那么保留下来的边集一定满足:
不存在环。若存在一个环且环外有别的点,则该环无法通过加边与环外的点连通。
图中每个点入度不超过 1 1 1 1 1 1
考虑贪心删掉不满足条件的边,显然对于一个入边数量大于 1 1 1 u u u
经过上述操作,可以得到一个由若干个链和环构成的新图。我们仍需打破得到的环来满足要求。
仍然考虑贪心,对于每个环,可以干掉环上的一条边,或者其替换为原图中指向该点的次优边。对于环上的每个点,其换边的代价即为当前最优入边的权值 减 次优入边的权值 。特别地,若仅有一条入边,代价即为该边权值。
特判初始即为一个大环的情况,因为此时我们无需将该环断掉重连。
Core Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 vector<vector<pair<int , int >>> in (n + 1 );for (int i = 1 ; i <= n; i++) {int a = read (), c = read ();emplace_back (make_pair (i, c));auto check = [&]() -> bool {for (int i = 1 ; i <= n; i++) {if (in[i].size () != 1 ) return 0 ;vector<char > vis (n + 1 , 0 ) ;int curr = 1 , cnt = 0 ;while (!vis[curr]) {1 ;if (cnt == n) return 1 ;else return 0 ;if (check ()) {0 << '\n' ;return 0 ;int sum = 0 ;vector<int > from (n + 1 ) ;for (int i = 1 ; i <= n; i++) {if (in[i].size () >= 1 ) {sort (in[i].begin (), in[i].end (), [](const pair<int , int >& x, const pair<int , int >& y){return x.second > y.second;0 ].second;0 ].first;vector<int > vis (n + 1 , 0 ) ; for (int i = 1 ; i <= n; i++) {if (vis[i] == 2 ) continue ;int curr = i;int > nodes;reserve (n);while (curr != 0 && vis[curr] == 0 ) {1 ;emplace_back (curr);if (curr != 0 && vis[curr] == 1 ) {int minn = numeric_limits<int >::max () / 2 ;bool flag = 0 ;for (int nw : nodes) {if (nw == curr) flag = 1 ;if (!flag) continue ;int diff = in[nw][0 ].second;if (in[nw].size () > 1 ) diff -= in[nw][1 ].second;min (minn, diff);for (int nw : nodes) {2 ;'\n' ;